Задача 28093 9.40. Диагонали вписанной в окружность...

slava191

29.05.2018

9.40. Диагонали вписанной в окружность трапеции взаимно перпендикулярны. Найдите площадь трапеции, если ее периметр равен 18, а основания относятся как 1:7.

SOVA

29.05.2018

★

Трапеция вписана в окружность, значит трапеция АВСD - равнобедренная.
AB=CD
и
AC=BD.

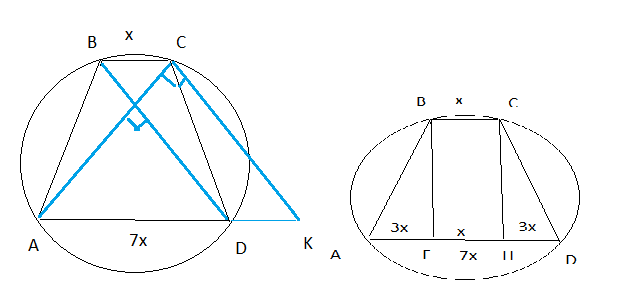
Пусть BC= х, AD=7x
Перенесем диагональ BD в точку С
CK || BD

Так как по условию диагонали трапеции перпендикулярны,
треугольник АСК - прямоугольный равнобедренный.
AC=BD=d
AK==x+7x=8x
По теореме Пифагора
AC^2+CK^2=AK^2
d^2+d^2=(8x)^2
d^2=32x^2
h( трапеции)=1/2) AK=4x

Проведем высоты из вершин верхнего основания на сторону AD
AF=HD=3x
По теореме Пифагора AB^2=(4x)^2+(3x)^2=(5x)^2
AB=CD=5x

Р( трапеции)=АВ+ВС+СD+AD=5x+x+5x+7x=18x
По условию Р( трапеции) =18
18х=18
x=1
Значит
BC=1; AD=7; h(трапеции)=4
S( трапеции)=(1+7)*4/2=16

О т в е т. 16