Задача 27997 4cos 3x+4cos 2x-3cosx-3=0 [2П;7П/2]...
Условие
предмет не задан
8055
Все решения
(4cos^3x+4cos^2x)-(3cosx+3)=0
4cos^2x*(cosx+1)-3*(cosx+1)=0
(cosx+1)*(4cos^2x-3)=0
cosx+1=0 ⇒ cosx = - 1 ⇒ х=(Pi)+2Pik, k ∈ Z
ИЛИ
4cos^2x-3=0
cosx=sqrt(3)/2 ⇒ x= ± (Pi/6)+2Pin, n ∈ Z
или
cosx= - sqrt(3)/2 ⇒ x= ± (5Pi/6)+2Pim, m ∈ Z
О т в е т.
(Pi)+2Pik, k ∈ Z
± (Pi/6)+2Pin, n ∈ Z
± (5Pi/6)+2Pim, m ∈ Z
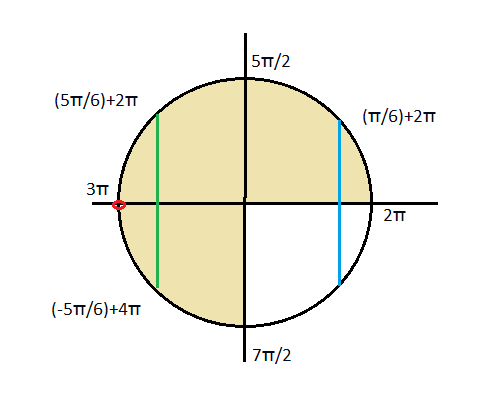
Указанному отрезку принадлежат 4 корня:
(Pi/6)+2Pi=13Pi/6
(5Pi/6)+2Pi=17Pi/6
(Pi)+2Pi=3Pi
(-5Pi/6)+4Pi=19Pi/6