Задача 27974 Вариант 3. 1. Основанием прямой...

u851406194

26 мая 2018 г.

Вариант 3.

1. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетом 5 см и гипотенузой 13 см. Высота призмы 8 см. Найдите площадь полной поверхности призмы.

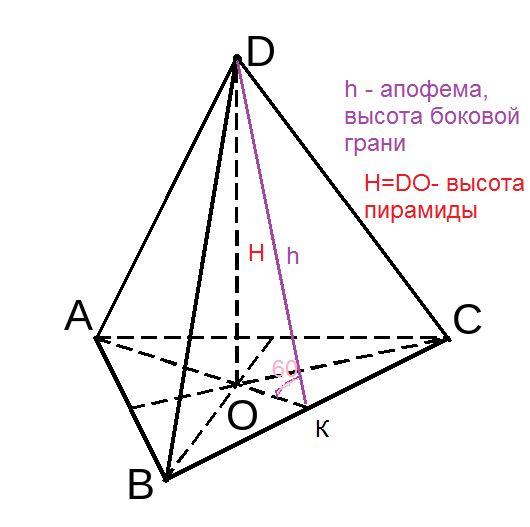
2. Апофема правильной треугольной пирамиды равна 4см и наклонена к плоскости основания под углом 60°. Найдите высоту пирамиды.

3. Основание прямоугольного параллелепипеда – квадрат. Найдите боковую поверхность параллелепипеда, если высота его равна 6 см, а диагональ параллелепипеда образует с плоскостью основания угол 45°.

4. Сторона основания правильной четырехугольной пирамиды равна 4см, а плоский угол при вершине пирамиды 60°. Найдите площадь полной поверхности пирамиды.

SOVA

26 мая 2018 г.

1) По теореме Пифагора второй катет
√13²–5²=√144=12 см
S(осн.)=(1/2)a·b=(1/2)5·12=30 кв см
S(бок)=Р(осн)·Н=(5+12+13)·8=30·8=240 кв см
S(полн)=S(бок) +2S (осн)=240+2·30=300
2)
H=h·sin60^o=4·(√3)/2)=2√3
см. рисунок.
3)
Треугольник АСС₁ – прямоугольный равнобедренный
СС₁=АС=6

АС²=AB²+BC²
AB=BC ( стороны квадрата равны)
36=2AB²
AB²=18
AB=3√2
S(бок)=P(осн)·Н=4·3√2·6=72 √3 кв. см

4)
Значит углы при основаниях в боковых треугольниках тоже по 60^o
Боковые треугольники – равносторонние
h( апофема)=4·√3/2=2√3
S(полн)=S(бок) +S (осн)= 4·S(боковых треугольников)+S (квадрата)=
=4·(1/2)·4·2√3+4²=16√3+16 ( кв. см)