Задача 27879 Найти общий интеграл дифференциального...
Условие
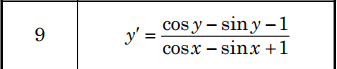
математика ВУЗ
838
Решение
★
dy/(cosy-sny-1)=dx/(cosx-sinx+1)
Интегрируем
∫ dy/(cosy-siny-1)= ∫ dx/(cosx-sinx+1)
Каждый интеграл ( см. интегрирование тригонометрических функций ) считается с помощью универсальной подстановки
tg(y/2)=t
Тогда
siny=2t/(1+t^2)
cosy=(1-t^2)/(1+t^20
y/2=arctgt
y=2arctgt
dy=2/(1+t^2)dt
∫ dy/(cosy-siny-1)=-∫dt/(t^2+t)=
=ln|1+t|-ln|t|
∫ dx/(cosx-sinx+1)=∫ds/(1-s)=-ln|s|
ln|1+tg(y/2)|-ln|tg(y/2)|=-ln|tg(x/2)+lnC - ответ.
Можно упростить