Задача 27867 4.2.78) Составить уравнение прямой,...
Условие
Решение
Прямая, симметричная данной, параллельна данной.
Значит ее уравнение имеет вид
x+2y- d=0
Чтобы найти d подставим координаты точки, принадлежащей этой прямой, например точки Е.
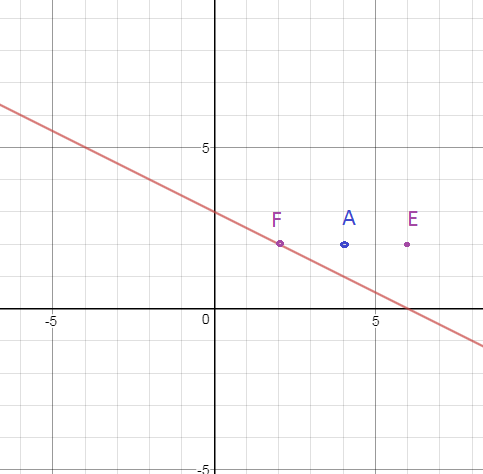
Для этого выберем точку F(2;2), принадлежащую данной прямой и найдем координаты точки Е симметричной относительно А
Е(6;2)
6+2*2-d=0
d=10
2 способ
Составим уравнение прямой, перпендикулярной данной и проходящей через точку А
vector{n}_(данной прямой)=(1;2)
vector{n}_(перпендикулярной прямой)=(2;-1)
Скалярное произведение этих векторов равно 0, векторы ортогональны.
2х-у+с=0
Чтобы найти c подставляем координаты точки А
2*4-2=с
с=-6
2х - у - 6 = 0
Найдем расстояние от точки А до данной прямой
d=|4+2*2-6|/sqrt(1+2^2)=2/sqrt(5)
Составим уравнение окружности с центром в точке А и радиусом R=2/sqrt(5).
Эта окружность касается данной прямой и второй прямой, параллельной данной и находящейся на расстоянии 2/sqrt(5) от точки.
(x-4)^2+(y-2)^2=4/5
Решаем систему уравнений
{(x - 4)^2 + (y - 2)^2 = 4/5
{2x - y - 6 = 0 ⇒ y = 2x - 6
(x-4)^2+(2x-6-2)^2=4/5
(x-4)^2=4/25
x-4=2/5 или х-4=-2/5
х=4,4 или х=3,6 - абсцисса точки М
у=2х-6=2*4,4-6=2,8
N(4,4; 2,8)
Прямая, параллельная данной имеет вид
х + 2y - d = 0
Чтобы найти d подставим координаты точки N
4,4+2*2,8 - d=0
d=10
О т в е т. х+2y -10 =0
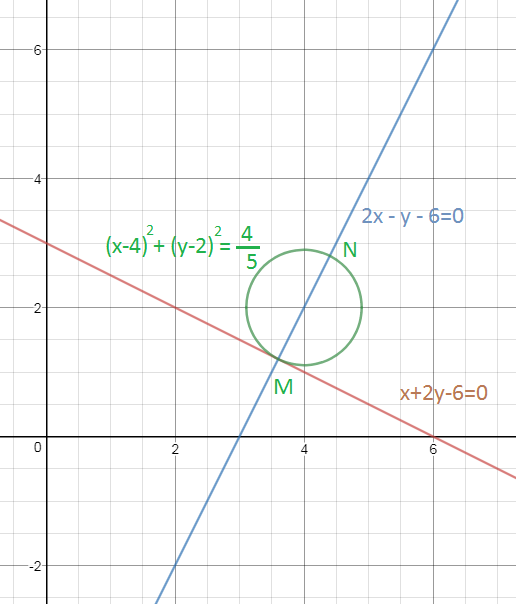
Все решения
