Задача 27865 9.25. Найдите острые углы прямоугольного...
Условие
Решение
В треугольнике ВСК биссектриса ВО делит сторону СК на части пропорциональные сторонам ВС и ВК
BC:BK=CO:OK=sqrt(3):sqrt(2)
BK=(sqrt(2)/sqrt(3))*b
Аналогично, для треугольника АСК
АК=(sqrt(2)/sqrt(3))*а
AK+KB=(sqrt(2)/sqrt(3))*(a+b)
По теореме Пифагора для треугольника АВС
a^2+b^2=(2/3)(a+b)^2⇒
3a^2+3b^2=2a^2+4ab+2b^2 ⇒
a^2-4ab+b^2=0
(a/b)^2-4*(a/b)+1=0
D=16-4=12
(a/b)=(4-2sqrt(3))/2=2-sqrt(3) или (a/b)=2+sqrt(3)
tg альфа =a/b=2-sqrt(3) или tg альфа =2+sqrt(3)
tg бета =b/a=2+sqrt(3) или tg бета =2-sqrt(3)
альфа =15 градусов; бета =75 градусов
или
альфа =75 градусов; бета = 15 градусов
так как
tg 75 градусов = tg (30 градусов + 45 градусов)=
=(tg 30 градусов + tg 45 градусов)/(1-tg30 градусов*tg 45 градусов)=((sqrt(3)/3)+1)/(1-sqrt(3)/3)=
=(sqrt(3)+3)/(3-sqrt(3))=(sqrt(3)+1)/(sqrt(3)-1)=
=(sqrt(3)+1)^2/(3-1)=(3+2sqrt(3)+1)/2=2+sqrt(3)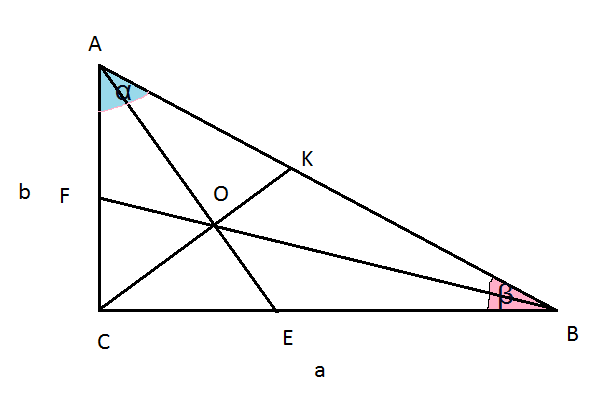
Все решения
