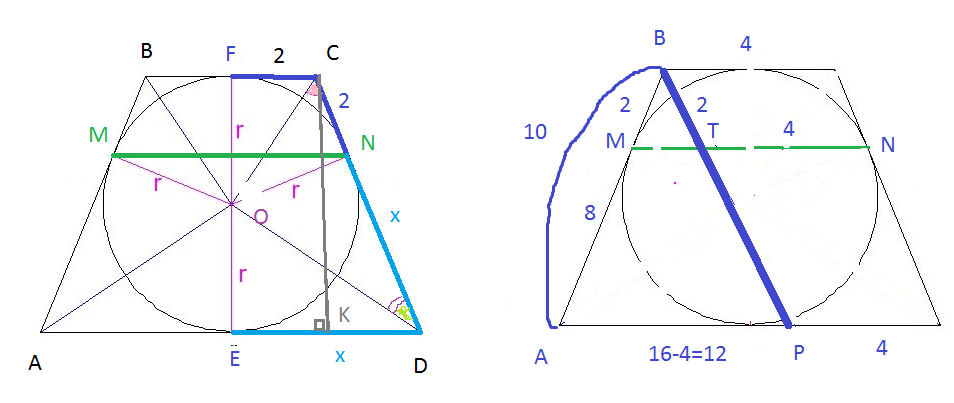
Задача 27864 9.23. Одно из оснований равнобедренной...

slava191

22.05.2018

9.23. Одно из оснований равнобедренной трапеции равно 4. Найдите расстояние между точками касания с ее боковыми сторонами вписанной в трапецию окружности ра­диуса 4.

SOVA

22.05.2018

★

Диаметр вписанной окружности равен 8, значит меньшее основание трапеции равно 4.
r=4
По свойству касательных к окружности, проведенных из одной точки, отрезки касательных равны.
FC=CN=2
DE=DN=x
Проводим высоту СК
КD=x-2
CD=x+2
CK=FE=2r=h
h=2*4=8
По теореме Пифагора
CK^2=CD^2-KD^2
8^2=(x+2)^2-(x-2)^2
64=(x+2-x+2)*(x+2+x-2)
64=4*2x
x=8

AD=2x=16

Проведем ВР || CD ( см. рис. справа)

Треугольник ВМТ подобен треугольнику АВР
2 : 10 = МТ : 12

МТ=2*12:10=2,4

MN=MT+TN=2,4+4=6,4

О т в е т. 6,4