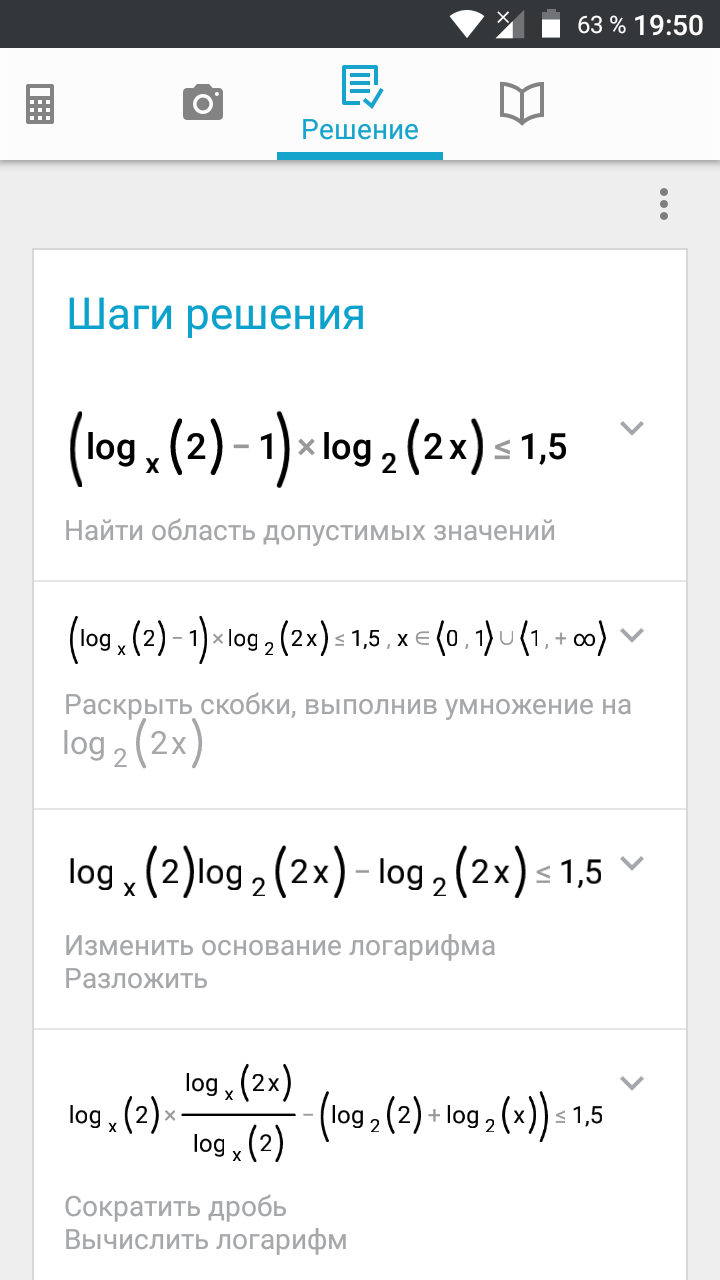
Задача 27823 Л15. Решите неравенство...
Условие
математика 10-11 класс
2718
Решение
★
x > 0
x ≠1
Замена переменной
log_(2)x=t
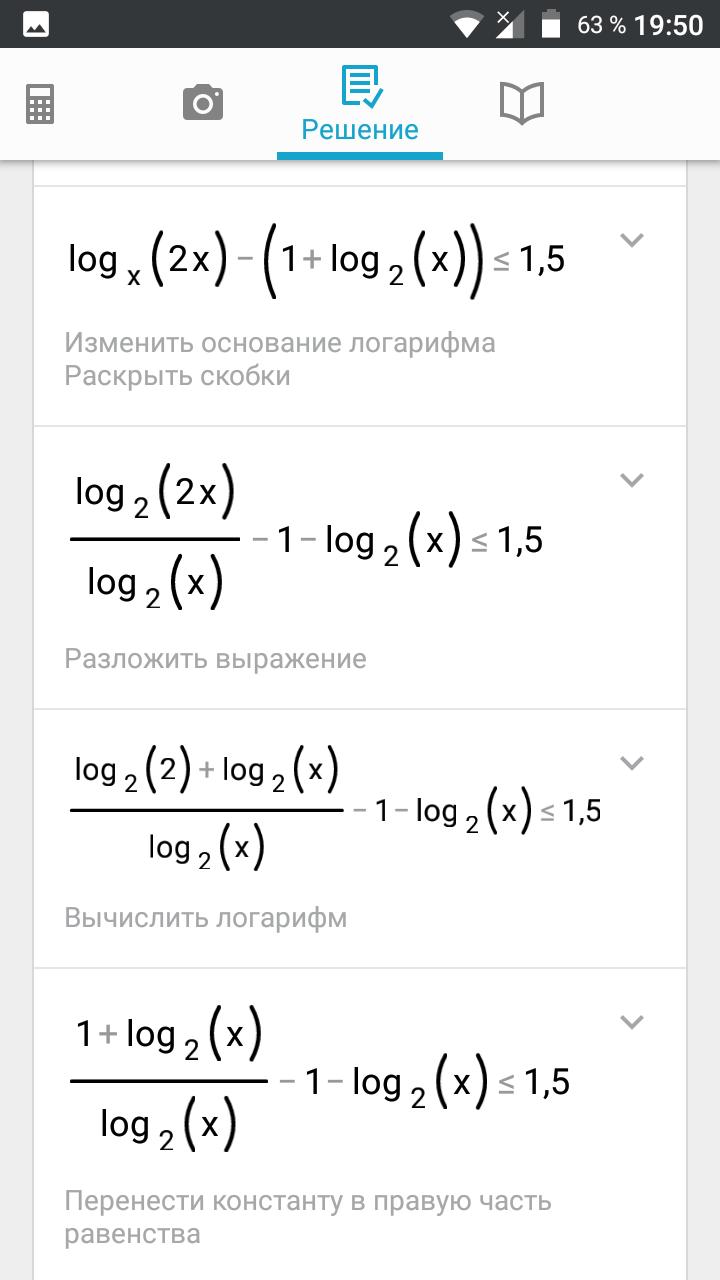
log_(2)(2x)=log_(2)2+log_(2)x =1+t
(log_(x)2-1)=(1/t)-1
Решаем неравенство
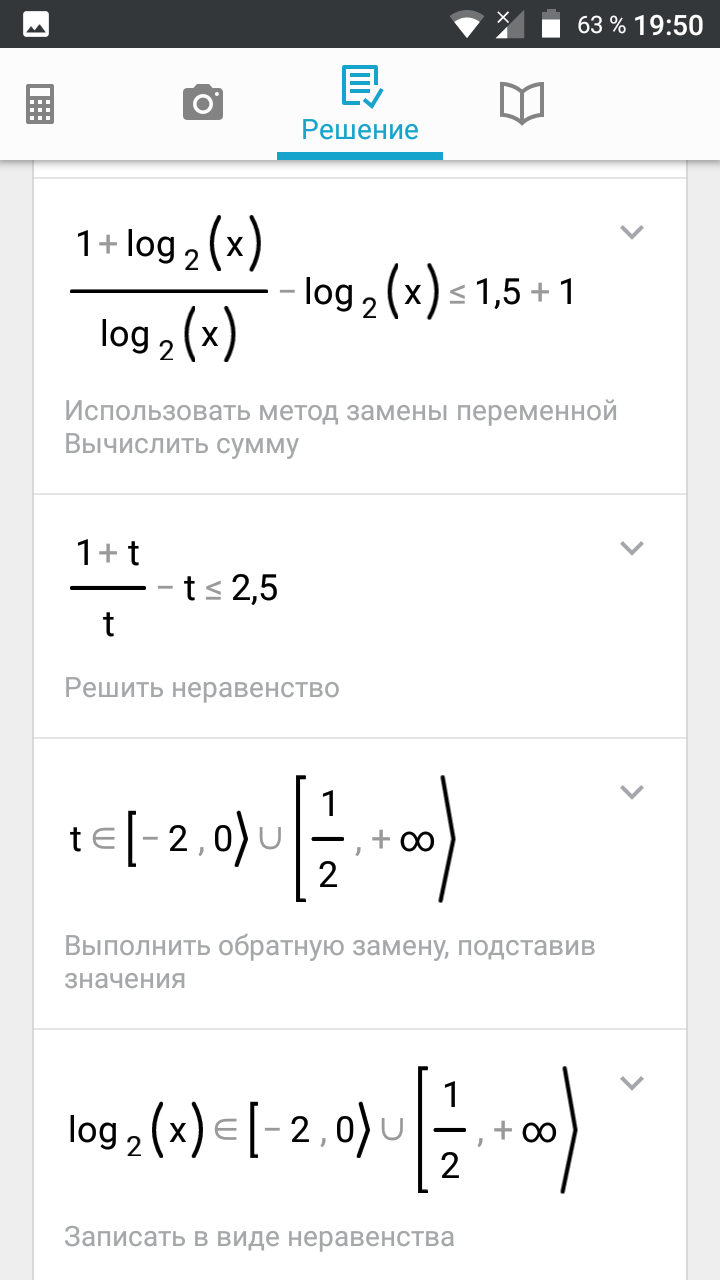
((1/t)-1)*(1+t) меньше или равно 3/2
(2t^2+3t-2)/(2t) больше или равно 0
D=9+16=25
корни -2 и 0,5
____ [-2] __+__ (0) ____ [1/2] __+__
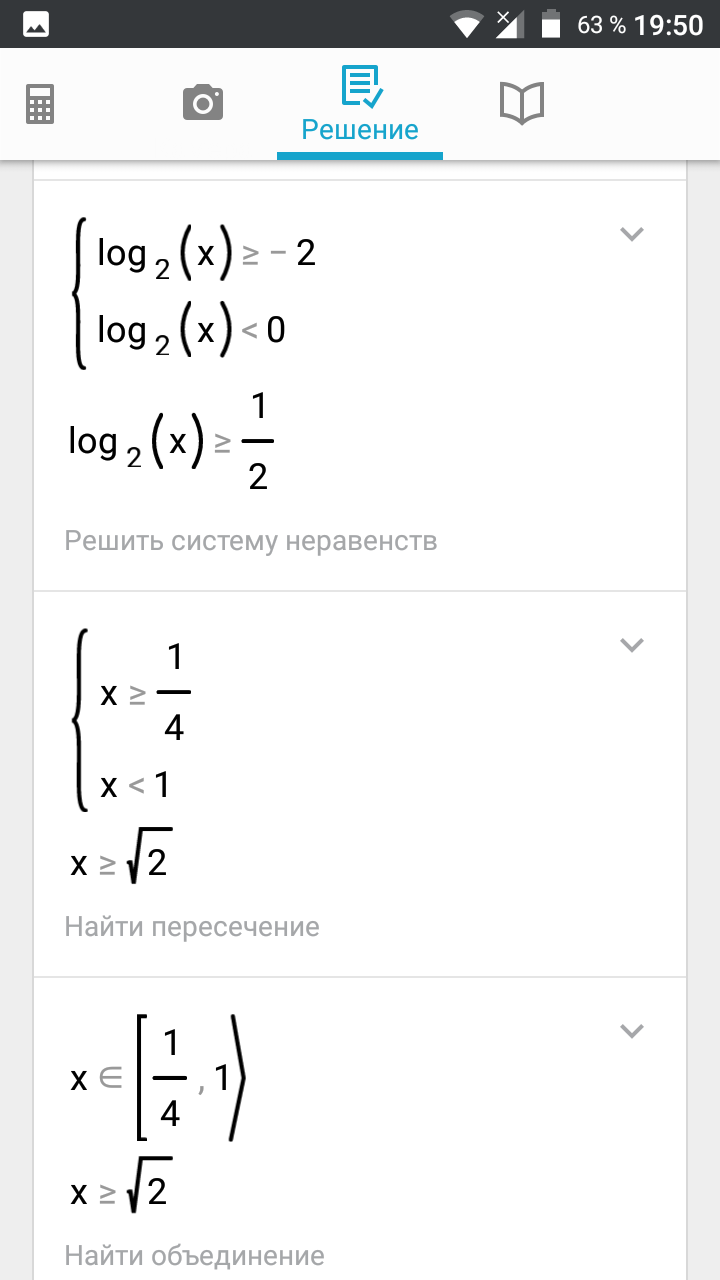
-2 меньше или равно log_(2) x < 0 или
log_(2)x больше или равно 1/2
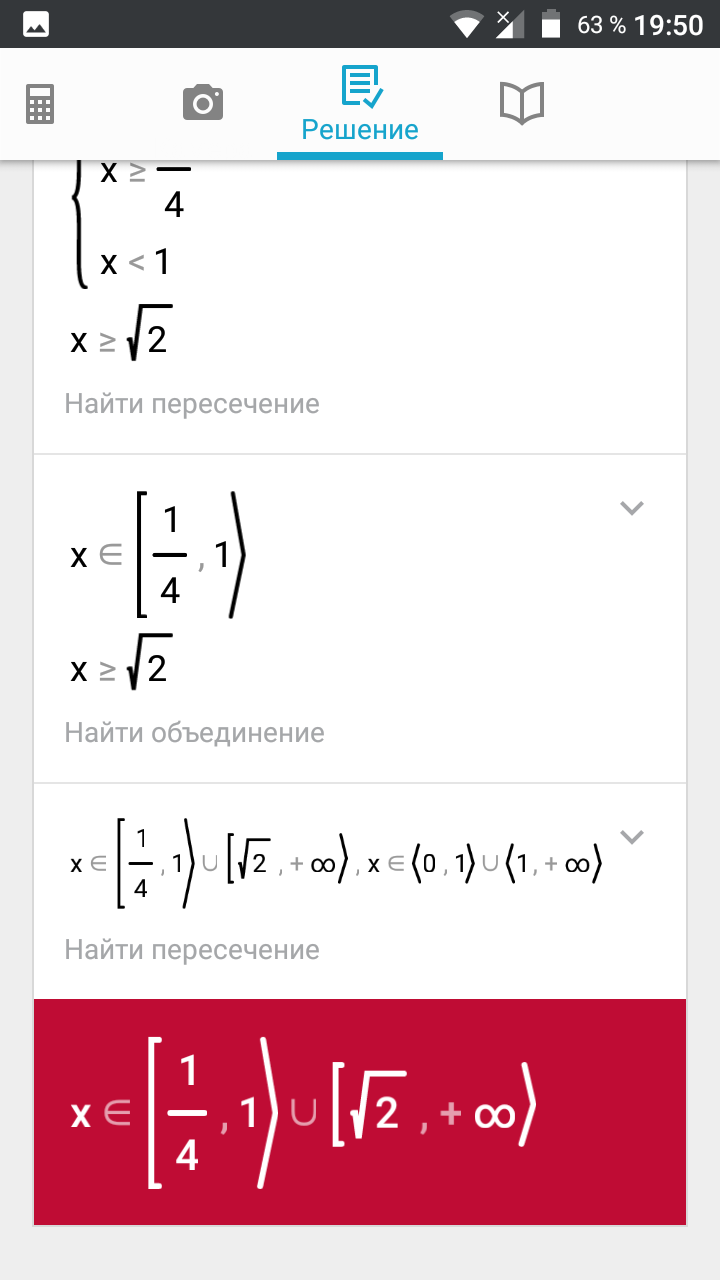
1/4 меньше или равно x < 1 или x больше или равно sqrt(2)
О т в е т. [1/4;1) U[sqrt(2);+ бесконечность)
Все решения