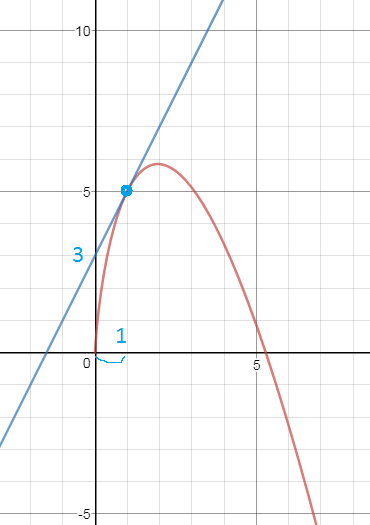
Задача 27807 Кривая проходит через точку А(1;5) и...

vk232428545

21 мая 2018 г.

Кривая проходит через точку А(1;5) и обладает тем свойством, что отрезок, отсеченный на оси ординат любой касательной равен утроенной абсциссе точки касания. Найти уравнение кривой.

SOVA

21 мая 2018 г.

★

Пусть (х;у) – произвольная точка на кривой.

Уравнение касательной к кривой, проведенной в точке (х;у) имеет вид

Y–y=(dy/dx)(X–x)

По условию

Y=3x; X=0

3x–y=(dy/dx)·(0–x)

или

y`–(1/x)y=–3 (#)

Линейное уравнение первого порядка

Решаем однородное уравнение
y–(1/x)y=0
dy/dx=y/x – уравнение с разделяющимися переменными
dy/y=dx/x
ln|y|=ln|x| +ln C⇒ y=C·x

Применяем метод вариации постоянной

y=C(x)·x
y`=C`(x)·x + C(x)

Подставляем в (#)

C`(x)·x + C(х)–(1/x)·(C(x)·x)=–3
или
C`(x)·x=–3
C`(x)=–3/x
С(х)=–3lnx+C

y=(–3lnx+C)·x
y=–3x·lnx+Cx

Чтобы найти С подставляем координаты точки

5=–3·1ln1+С

С=5

О т в е т.y=–3xlnx+5x