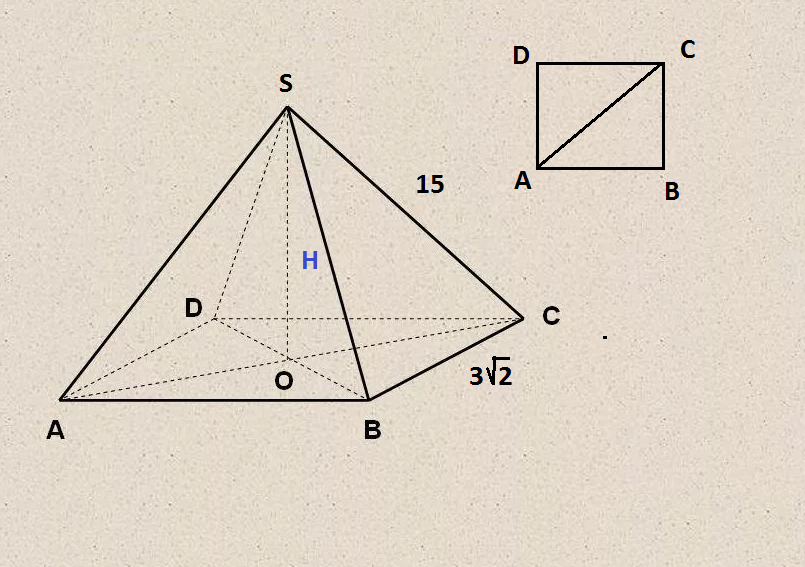
Задача 27790 ...

u851406194

21.05.2018

В правильной четырёхугольной пирамиде SABCD с основанием ABCD боковое ребро SC = 15, сторона основания равна 3√2. Найдите объём пирамиды.

SOVA

21.05.2018

★

АС=3sqrt(2)*sqrt(2)=6 - диагональ квадрата со стороной 3sqrt(2)
OC=(1/2)AC=3
По теореме Пифагора
SO^2=SC^2-OC^2=15^2-3^2=216
H=SO=sqrt(216)=6sqrt(6)

V=(1/3)*S(осн.)*Н=(1/3)*(3sqrt(2))^2*6sqrt(6)=36sqrt(6)