Задача 27727 Постройте график функции y=|x2x6|. Какое...

u83220236150

19.05.2018

Постройте график функции y=|x2−x−6|. Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?

SOVA

21.05.2018

y=x^2-x-6 - парабола, ветви вверх, вершина в точке с абсциссой х_(o)=1/2
y_(o)=(1/2)^2-(1/2)-6=-6 целых 1/4=-25/4

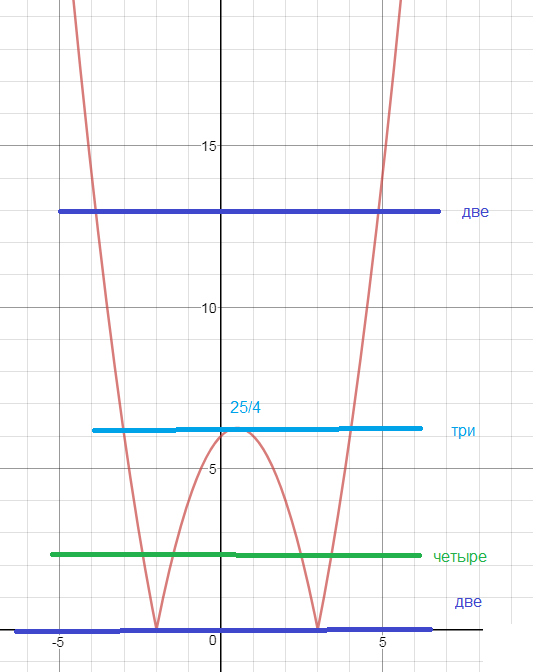
График y=|x^2-x-6| - получаем из графика y=x^2-x-6 отражением относительно оси Ох части графика, расположенной в нижней полуплоскости ( см. рис)


О т в е т. Наибольшее число точек - четыре