Задача 27532 Решите уравнение 5sin^2x+6cosx+6=0...

vk383998546

15.05.2018

Решите уравнение 5sin^2x+6cosx+6=0
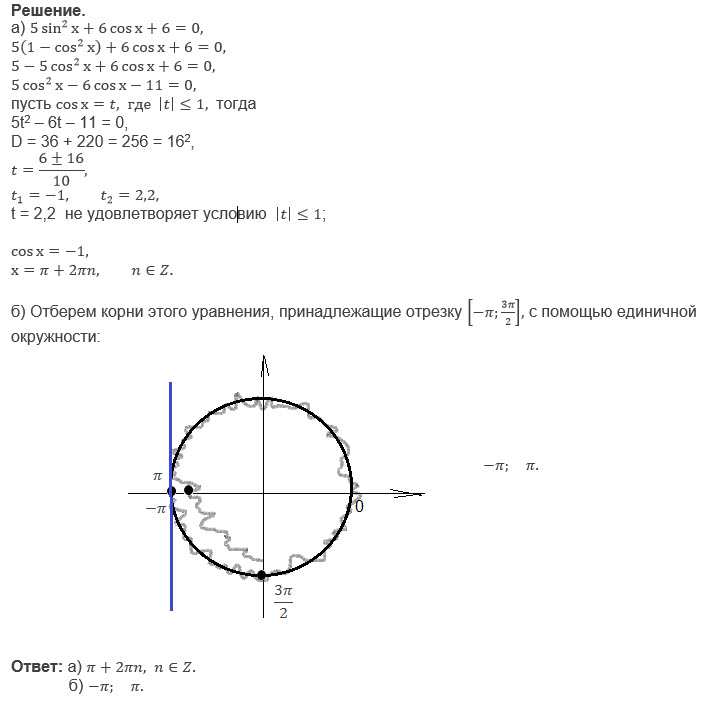
Найдите все корни принадлежащие отрезку минус Пи; 3Пи/2

vk397114329

15.05.2018

5sin^2(x)+6cosx+6=o
5(1-cos^2(x)+6cosx+6=0;
5cos^2(x)-6cosx-11=0. Пусть cosx=t. |t| < =1. тогда
5t^2-6t-11=0; D=64. t1=(3+8)/5=11/5-не удовлетворяет условию |t| < =1; t2=(3-8)/5=-1 .тогда cosx=-1. x=pi+2pi*k. k-целое число. Отберем корни:
-pi < =pi+2pik < =3pi/2;
-1 < =1+2k < =3/2;
-1 < =k < =1/4; k=-1; k=0
Соответственно x1=-pi; x2=pi.
Ответ: a) x=pi*(1+2k).k-целые числа
b) -pi;pi.

К.Тёмный

15.05.2018

a)5(1-cos^2x)+6cosx+6=0 |*(-1)
5cos^2x-6cosx-11=0
замена:
cosx=t , t ∈[-1;1]
5t^2-6t-11=0
t=-1/5 t=2.2( нет решений)
обр.замена
cosx=-1/5
x=+- 2п/3 + 2Пn,n ∈ z
б)-П меньше или равно- 2п/3 + 2Пn меньше или равно 3п/2
n=1 x=4П/3


-П меньше или равно 2п/3 + 2Пn меньше или равно 3п/2
нет.