Задача 27437 Л17. В 2016 году в НИИ «Наномир»...
Условие
С 1 января 2017 года 4 инженера ушли на заслуженный отдых. Чтобы сохранить среднюю зарплату по НИИ на уровне прошлого года, директор решил изменить зарплату только у своих замов.
В конце 2017 года неожиданно выяснилось, что годовой фонд заработной платы НИИ, сформированный в объеме прошлого года, оказался выбран не полностью. В связи с этим все оставшиеся на счету фонда деньги директор перечислил себе в качестве премии.
Определите:
а) среднюю зарплату по НИИ в 2017 году;
б) на сколько % изменилась (увеличилась или уменьшилась) зарплата заместителей директора НИИ в 2017 году;
в) размер премии, полученной директором НИИ в конце 2017 года
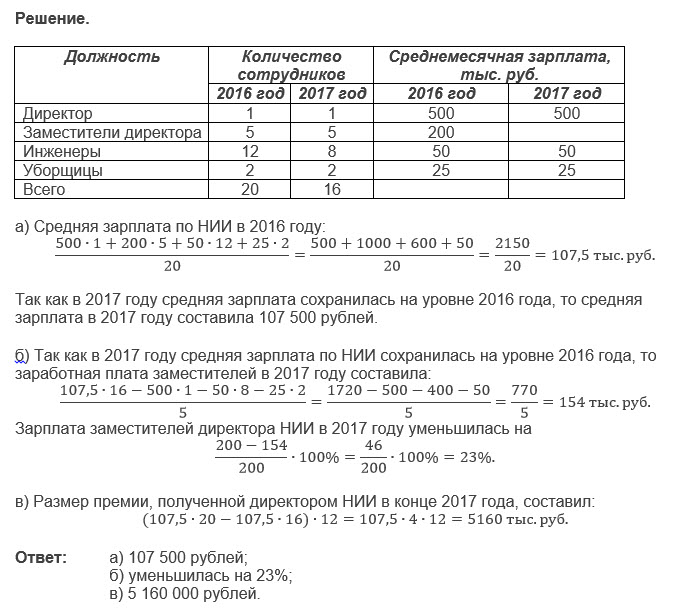
Решение