Задача 27367 9^(x-1)/(9^(x-1)-1) больше или равно...
Условие
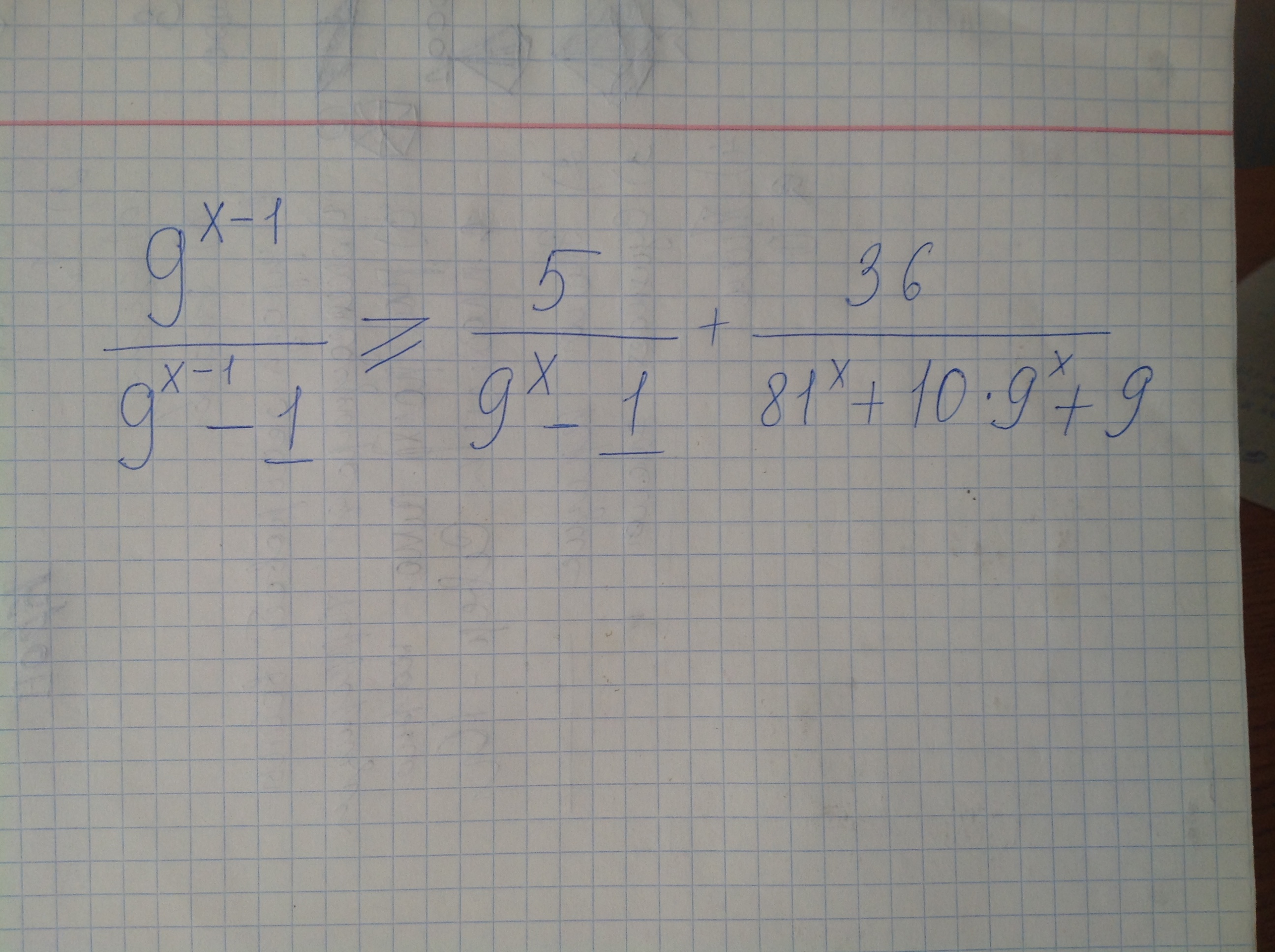
предмет не задан
750
Решение
★
9^x=t
t > 0 при любом х
Так как
9^(x-1)/(9^(x-1)-1)=9*(9^(x-1))/(9*(9^(x-1)-1))=9^(x)/(9^(x)-9),
неравенство примет вид:
t/(t-9) больше или равно (5/(t-1))+(36/(t^2+10t+9))
t^2+10t+9=0
D=100-4*9=64
t=(-10-8)/2=-9 или t=(-10+8)/2=-1
t^2+10t+9=(t+9)(t+1)
t/(t-9) - (5/(t-1)) - (36/(t+1)(t+9)) больше или равно 0
((t^2-t-5t+45)(t^2+10t+9) - 36*(t^2-10t+9))/((t^2-1)(t^2-81)) больше или равно 0
...
По-моему в условии опечатка.
Знаменатель последней дроби
не 81^x+10*9^x+9
а 81^x-10*9^x+9