Задача 27354 Неравенство...
Условие
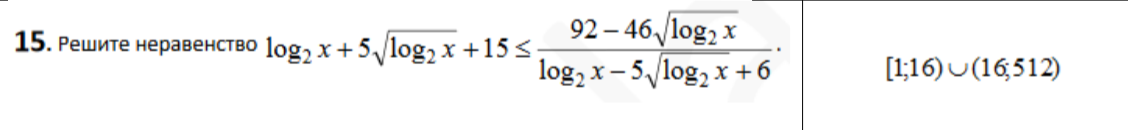
математика 10-11 класс
471
Решение
★
{x > 0
{log_(2)x больше или равно 0 ⇒ x больше или равно 1
{log_(2)x-5sqrt(log_(2)x)+6 ≠ 0 ⇒ sqrt(log_(2)x) ≠ 2 и sqrt(log_(2)x) ≠ 3 ⇒ х ≠ 2^4 и х ≠ 2^(9)
Замена переменной
sqrt(log_(2)x)=t
t больше или равно 0
Неравенство принимает вид
t^2+5t+15 меньше или равно 46(2-t)/((t-2)(t-3));
t^2+5t+15 + (46/(t-3)) меньше или равно 0
(t^3+2t^2+1)/(t-3) меньше или равно 0
При t > 0
t^3+2t^2+1 > 0
t < 3
Обратная замена
sqrt(log_(2)x) < 3
log_(2)x < 9
x < 512
С учетом ОДЗ получаем ответ
[1;16)U(16;512)