Задача 27071 4.64) tg^3x+tg^2x-3tgx-3 = 0, [2Pi;...
Условие
Решение
(-1)^3+(-1)^2-3*(-1)-3=0 ⇒ 0=0 - верно.
Значит можно разложить левую часть уравнения на множители, один из которых нам известен.
Это (tgx+1)
Искусственный прием: прибавить и отнять 1:
tg^3x+1+tg^2x-1-3tgx-3=0
(tgx+1)*(tg^2-tgx+1)+(tgx-1)*(tgx+1)-3*(tgx+1)=0
(tgx+1)*(tg^2x-tgx+1+tgx-1-3)=0
[b](tgx+1)*(tg^2x-3)=0 [/b]
tgx+1=0 ⇒ tgx =-1 ⇒ x=(-Pi/4)+Pik, k ∈ Z
или
tg^2x-3=0 ⇒ tgx =-sqrt(3) или tgx =sqrt (3) ⇒
x=(-Pi/3)+Pin, n ∈ Z или ⇒ x=(Pi/3)+Pim, m ∈ Z
О т в е т:
а)(-Pi/4)+Pik, k ∈ Z
± (Pi/3)+Pim, m ∈ Z
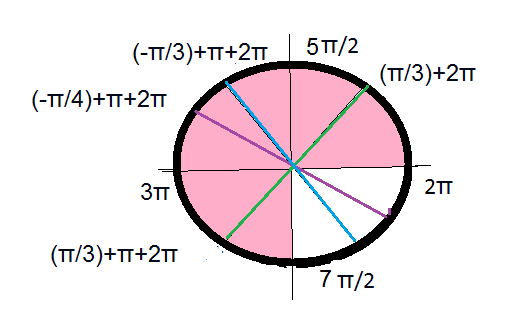
б)(Pi/3)+2Pi=7Pi/3 ∈ [2π; 7π/2]
(-Pi/3)+Pi+2Pi=8Pi/3 ∈ [2π; 7π/2]
(-Pi/4)+Pi+2Pi=11Pi/4∈ [2π; 7π/2]
(Pi/3)+Pi+2Pi=10Pi/3 ∈ [2π; 7π/2]