Задача 27066 4.57) 2cos^22x-(2+sqrt(2))cos2x+sqrt(2)...
Условие
математика 10-11 класс
806
Решение
★
cos 2x = t
2t^2-(2+√2)t+√2 > 0
D=(2+√2)^2-4*2*√2=[b]4+4√2+2-8√2=(4-4√2+2)[/b]=(2-√2)^2
t_(1)=((2+√2)-(2-√2))/4= √2/2 или t_(2)=((2+√2)+(2-√2))/4= 1
__+__ ( √2/2 ) __-___ (1) _+__
cos2x < √2/2 или cos2x > 1 ( не имеет решений, так как
|cos2x| меньше или равно 1)
cos2x < √2/2
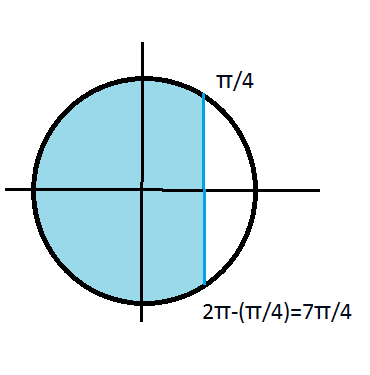
(Pi/4)+2Pin < 2x < (2Pi)-(Pi/4)+2Pin, n ∈ Z
(Pi/4)+2Pin < 2x < (7Pi/4)+2Pin, n ∈ Z
(Pi/8)+Pin < x < (7Pi/4)+Pin, n ∈ Z
О т в е т. (Pi/8)+Pin < x < (7Pi/4)+Pin, n ∈ Z