Задача 27065 4.56) 2sin^2x+2=3sqrt(2)cos(Pi/2+x),...
Условие
математика 10-11 класс
766
Все решения
cos(π/2+x)=-sinx
Уравнение принимает вид:
2sin^2x+2= - 3√2sinx
2sin^2x+3√2sinx+2=0
D=(3√2)^2-4*2*2=18-16=2
корни (-3√2 ± √2)/4
sinx=-√2/2 ⇒ x=(-1)^(k)(-Pi/4)+Pik, k ∈ Z
или
sinx=-√2 - уравнение не имеет корней, так как |sinx| меньше или равно 1, а √2 > 1
О т в е т
а)(-1)^(k+1)(Pi/4)+Pik, k ∈ Z
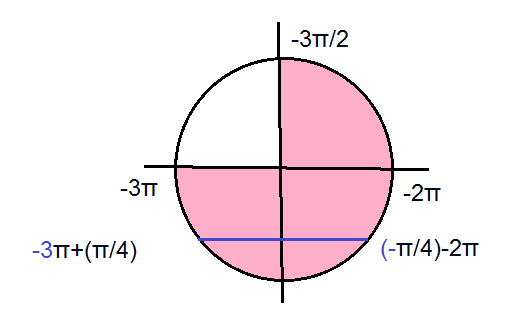
б) x=(-Pi/4)-2Pi=-9Pi/4∈[–3π; –3π/2]
x=(Pi/4)-3Pi=-11Pi/4∈[–3π; –3π/2]