Задача 27063 ...

vk373959827

03.05.2018

1) Основанием пирамиды является правильный треугольник две боковые грани пирамиды перпендикулярны плоскости основания A третья образует с плоскостью основания угол 60 градусов. Чем равна площадь полной поверхности пирамиды если ее высота равна 24 см?

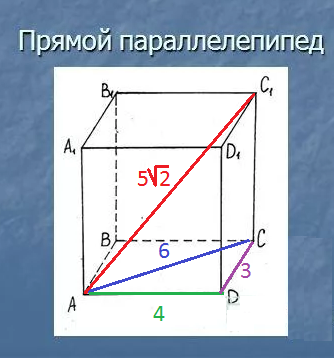
2) Диагональ АС1 прямого параллелепипеда АВСDA1B1C1D1 равна 5√2 см. диагональ основания AC-6 см a стороны основания 3 см и 4 см. Чем равна площадь диагонального сечения которое проходит через вершины В и D?

SOVA

03.05.2018

★

1.
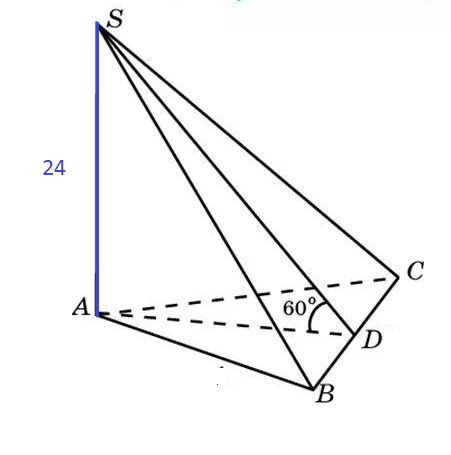
Из прямоугольного треугольника SAD
tg∠ADS=AS/AD
AD=AS/tg60^(o)=24*2/sqrt(3)=16sqrt(3)

SD=32sqrt(3)
катет против угла в 30 градусов равен половине гипотенузы, значит гипотенуза в два раза больше катета.
В равностороннем треугольнике АВС
AD=16sqrt(3)
AB=BC=AC=32

S=S( ΔABC)+S(ΔSAB)+S(ΔSAC)+S(ΔSBC)=

=(32*sqrt(3)/4)+2*(1/2)32*24+(1/2)*12*32sqrt(3)=
=200 sqrt(3)+786


2.В основании прямого параллелепипеда - параллелограмм АВСD

По формуле
АС^2+BD^2=2*AB^2+2CD^2
находим ВD
BD=sqrt(14)

H^2=(5sqrt(2))^2-6^2=14
H=sqrt(14)

S(BDD1B1)=BD*H=14