Задача 26990 4.54) 20sin^2x+9cosx < 21...
Условие
математика 10-11 класс
2491
Все решения
20*(1-cos^2x)+9cosx-21 < 0
-20 cos^2x+9cosx-1 < 0
20cos^2x-9cosx+1 > 0
D=81-4*20=1
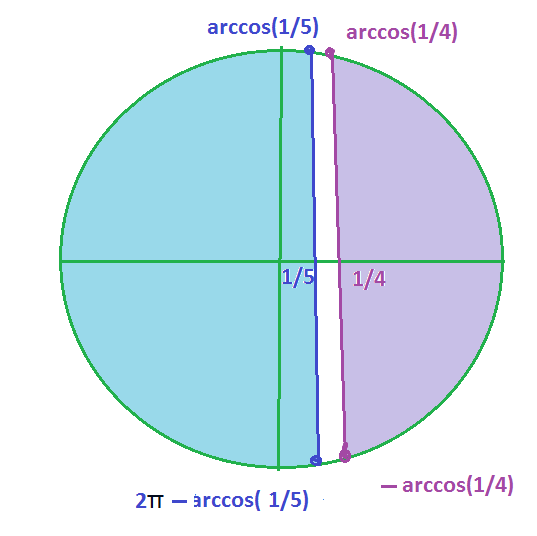
cosx < 1/5 или cosx > 1/4
cosx < 1/5
arccos(1/5)+2Pi < x < 2Pi-arccos(1/5)+2Pin=-arccos(1/5)+2Pi(n+1), n ∈ Z
или
cosx > 1/4
-arccos(1/4)+2Pim < x < arccos(1/4)+2Pim, m ∈ Z
О т в е т.
-arccos(1/4)+2Pim < x < arccos(1/4)+2Pim, m ∈ Z
arccos(1/5)+2Pi < x < 2Pi-arccos(1/5)+2Pin=-arccos(1/5)+2Pi(n+1), n ∈ Z