Задача 26972 cos^2 2x+9cos^2...

u14525511180

01.05.2018

cos^2 2x+9cos^2 3x-6cos2xcos3x-8cosx+24cos3x=-16

SOVA

02.05.2018

Решение в случае
cos^2 2x+9cos^2 3x–6cos2xcos3x–8cos2x+24cos3x=–16

(сos2x-3cos3x)^2-8(cos2x-3cos3x)+16=0
(cos2x-3cos3x+4)^2=0
cos2x-3сos3x+4=0
cos2x-3cos3x=-4
Так как
-1 меньше или равно cos2x меньше или равно 1
-3 меньше или равно -3cos3x меньше или равно 3
-4 меньше или равно cos2x-3cos3x меньше или равно 4
равенство - 4 возможно лишь при

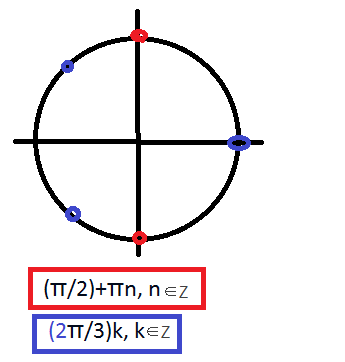
{cos2x=-1⇒ 2x=(Pi)+2Pin, n∈ Z⇒ x=(Pi/2)+Pin, n∈ Z
{-3cos3x=-3 ⇒ cos3x =1 ⇒ 3x=2Pik, k∈ Z ⇒ x=(2P/3)ik, k∈ Z

Пересечение полученных множеств ( решений) даст ответ. ( см. рис.)

Множества не пересекаются.
Ответ нет решений.