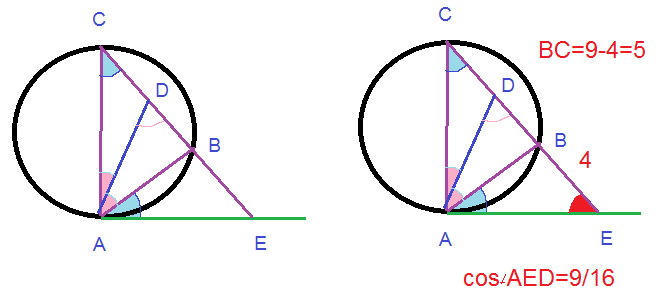
Задача 26931 16. Касательная в точке А к описанной...

slava191

29.04.2018

16. Касательная в точке А к описанной окружности треугольника АВС пересекает прямую ВС в точке Е, AD - биссектриса треугольника АВС.

А) Докажите, что АЕ=ЕD

Б) Известно, что точка Е лежит на луче СВ и СЕ=9, ВЕ=4, cos AED = 9/16. Найдите расстояние от вершины В до прямой АС.

SOVA

30.04.2018

а)
∠ АСB - вписанный в окружность, он измеряется половиной дуги АС.
∠ ЕАB - угол между касательной АЕ и хордой АВ, измеряется половиной дуги АС.
Значит ∠ АСB= ∠ ЕАB= альфа.

∠ СAD= ∠ BAD = бета ( АD биссектриса ∠ ВАС)

∠ ЕАD= ∠ЕАВ + ВAD= [b]альфа + бета[/b]
∠ АDE=∠ DАВ+ ∠СAD=[b]альфа + бета[/b] ( внешний угол треугольника АСD.
∠ ЕАD=∠ АDE=альфа + бета

Значит треугольник ЕАD равнобедренный,
[b] АЕ=ЕD.[/b]

б)
CE*BE=AE^2 - [b] произведение секущей на ее внешнюю часть равно квадрату касательной [/b]
9*4=AE^2
AE=6
По теореме косинусов из треугольника АВЕ
АВ^2=АЕ^2+BE^2-2*AE*BE*cos∠ AEB=6^2+4^2-2*6*4*(9/16)=52-27=25
AB=5

По теореме косинусов из треугольника АCЕ
АC^2=АЕ^2+CE^2-2*AE*CE*cos∠ AEB=6^2+9^2-2*6*9*(9/16)=117-(243/4)=225/4
AC=15/2=7,5
Треугольник АВС равнобедренный
АВ=ВС=5
ВК ⊥ АС
Высота ВК равнобедренного треугольника одновременно и медиана.
АК=КС=15/4
По теореме Пифагора
ВК^2=AB^2-AK^2=5^2-(15/4)^2=(400-225)/16=175/16
h=BK=5sqrt(7)/4
О т в е т. 5sqrt(7)/4