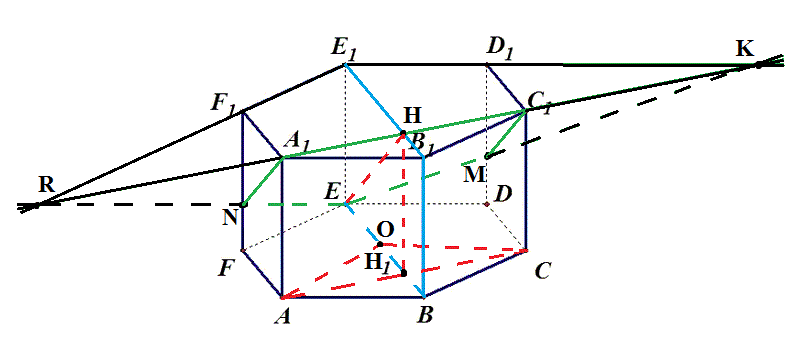
Задача 26929 Л14) В правильной шестиугольной призме...
Условие
а) Докажите, что плоскость A1С1E перпендикулярна плоскости BB1E1.
б) Найдите угол между плоскостями A1C1E и ABC .
Решение
Проведем A_(1)C_(1), пусть A_(1)C_(1) пересекает E_(1)D_(1) в точке K, а EK пересекает DD_(1) в точке M, соединяем C_(1)M.
Аналогично, пусть A_(1)C_(1) пересекает E_(1)F_(1) в точке R, а ER пересекает FF_(1) в точке N, соединяем A_(1)N.
В итоге мы получаем, что (A_(1)NEMC_(1)) - это и есть наша плоскость (A_(1)C_(1)E)
Соединяем B_(1)E_(1). Т.к. плоскости основания параллельны, то через B мы проводим прямую параллельную B_(1)E_(1).
(BB_(1)E_(1)E) - это и есть плоскость (BB_(1)E).
Пусть B_(1)E_(1) и A_(1)C_(1) пересекаются в точке H, проведем HE.
Вот мы и построили плоскости и линию их пересечения HE.
2) Как мы докажем что они между собой перпендикулярны?!
Что у нас есть:
У нас A_(1)C_(1) ⊥ E_(1)B_(1) из-за того, что в основании правильный шестиугольник.
С другой стороны у нас A_(1)C_(1) ⊥ BB_(1), т.к. дана собственно правильная призма, т.е. ребра ⊥ основанию.
Исходя из вышесказанного, можно смело утверждать, что A_(1)C_(1) ⊥ плоскости (BB_(1)E_(1)E), т.к. она ⊥ двум пересекающимся прямым в этой плоскости.
Ну а далее у нас плоскость (A_(1)C_(1)E) проходит через прямую A_(1)C_(1), а это означает, что в данном случае соблюдается признак ⊥ двух плоскостей и мы пункт а) доказали.
(A_(1)С_(1)E) ⊥ (BB_(1)E_(1)) ч.т.д.
б) Опустим HH_(1) ⊥ (ABC), она упадет сразу на середину AC.
Пусть O - это центр основания. HH_(1) = AA_(1) = 5.
Отрезок OE = AB = 4, т.к. OE - это радиус окружности описанной около правильного шестиугольника, а он равен стороне этого шестиугольника.
Достоим AO и OC, получаем ромб AOCB ⇒
OH_(1) = H_(1)B = OE / 2 = 2.
В таком случае весь отрезок EH_(1) = 6, ну и тогда tg(H_(1)EH) = HH_(1) / EH_(1) = 5/6.
Следовательно тогда сам угол составляет: arctg(5/6)
Ответ: arctg(5/6)