Задача 26928 Л13. А) Решите уравнение...
Условие
Б) Найдите все корни этого уравнения, принадлежащие промежутку [3Pi/2; 3Pi]
Решение
cos(13π/2–x)=cos(6π+(π/2)–x)=cos((π/2)–x)=sinx
(5/sin^2x)+(7/sinx) - 6 =0
(5+7sinx-6sin^2x)/sin^2x=0
{5+7sinx-6sin^2x=0
{sin^2x ≠ 0 ⇒ sinx ≠ 0 ⇒ x ≠ Pik, k ∈ Z
6sin^2x-7sinx-5=0
D=(-7)^2-4*6*(-5)=49+120=169
sinx=5/3 - уравнение не имеет корней,
так как |sinx| меньше или равно 1
5/3 > 1
sinx=-1/2
x=(-1)^k arcsin(-1/2)+Pik, k ∈ Z
x=(-1)^k *(-Pi/6)+Pik, k ∈ Z
можно записать в виде серии двух ответов
x=(-Pi/6)+2Pik или х=Pi+(Pi/6)+2Pik=(7Pi/6)+2Pik, , k ∈ Z
Указанному отрезку принадлежит корень
х=(-Pi/6)+2Pi=11Pi/6
3Pi/2=9Pi/6 < 11Pi/6 < 18Pi/6=3Pi
О т в е т.
a)x=(-1)^k *(-Pi/6)+Pik, k ∈ Z
б)11Pi/6 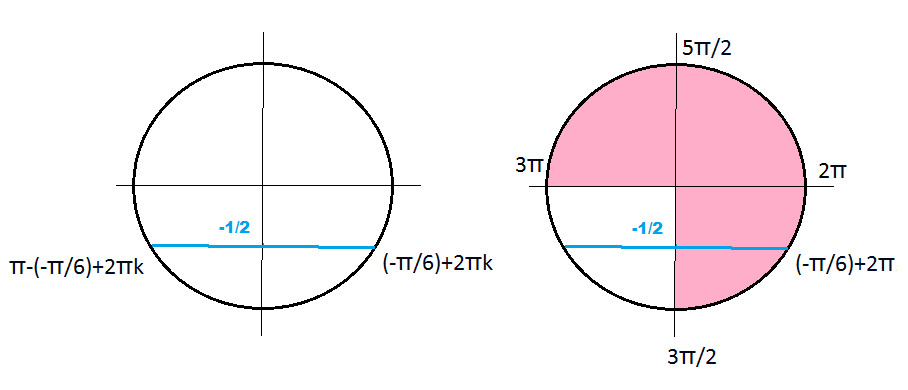
Все решения
