Задача 26924 Л8. Объем треугольной пирамиды равен 15....

slava191

29.04.2018

Л8. Объем треугольной пирамиды равен 15. Плоскость проходит через сторону основания этой пирамиды и пересекает противоположное боковое ребро в точке, делящей его в отношении 1:2, считая от вершины пирамиды. Найдите больший из объемов пирамид, на которые плоскость разбивает исходную пирамиду.

SOVA

29.04.2018

★

V( пирамиды SABC)=(1/3) S (Δ АВС) * SM
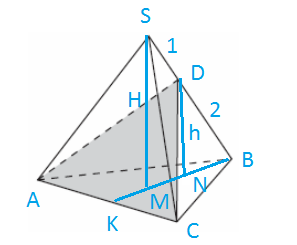
SM=H
V( пирамиды SABC)=(1/3) S (Δ АВС)*Н
V( пирамиды DABC)=(1/3) S (Δ АВС) * DN
DN=h
V( пирамиды DABC)=(1/3) S (Δ АВС) * h

Из подобия треугольников SMB и DNB
H:h=3:2
h=2H/3

V( пирамиды DABC)=(1/3) S (Δ АВС) * h=(1/3)S (Δ АВС) *(2/3)H=(2/3)*V(пирамиды SABC)=(2/3)*15=10
Оставшаяся часть имеет объем 5.
Он меньше чем 10.
О т в е т. 10