Задача 26911 4.10) 4sin^4(x/2)+12cos^2(x/2)=7...
Условие
Решение
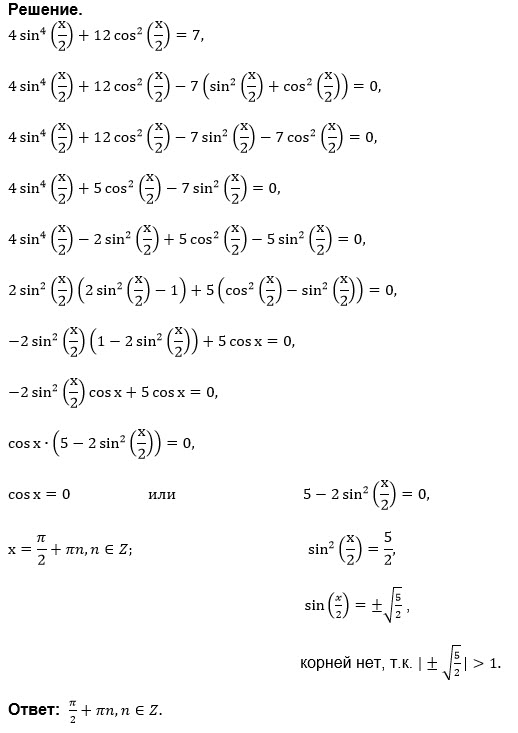
Все решения
4sin^4(x/2)+12*(1-sin^2(x/2))=7
4sin^4(x/2)-12*sin^2(x/2))+5=0
sin^2(x/2)=t
4t^2 -12t+5=0
D=144-4*4*5=64=8^2
t=(12-8)/8=1/2 или t=(12+8)/8=5/2
sin^2(x/2)=(5/2) ⇒ sin(x/2)=± sqrt( 5/2)
уравнения
sin(x/2)= - sqrt( 5/2) и sin(x/2)= sqrt( 5/2)
не имеют корней в силу ограниченности косинуса и синуса
|sinx| меньше или равно 1;
|cosx| меньше или равно 1;
sqrt(5/2) > 1
sin^2(x/2)=1/2 ⇒ sin(x/2)=-sqrt(2)/2 или sin(x/2)=sqrt(2)/2
sin(x/2)=-sqrt(2)/2 ⇒ (x/2)=(-1)^k*(-Pi/4)+Pik, k ∈ Z ⇒
x=(-1)^k(-Pi/2)+2Pik, k ∈ Z
при k=2m
x=(-Pi/2)+2Pim, m ∈ Z
при k=2m+1
x=(5Pi/2)+2Pim, m ∈ Z
ИЛИ
sin(x/2)=sqrt(2)/2 ⇒ (x/2)=(-1)^n*(Pi/4)+Pin, n ∈ Z ⇒
x=(-1)^n(Pi/2)+2Pin, n ∈ Z ⇒
при n=2m
x=(Pi/2)+4Pim,
при n=2m+1
x= (3Pi/2)+4Pim,
m ∈ Z
О т в е т.
(-Pi/2)+2Pim, (Pi/2)+4Pim, (3Pi/2)+4Pim,(5Pi/2)+2Pim, m ∈ Z