Задача 26899 Все на картинке...
Условие
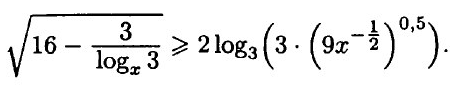
Решение
x > 0; x ≠ 1
log_(x)3=1/log_(3)x
log_(3)(3*(9*x^(-1/2))^(0,5))=log_(3)(3*9^(0,5)*x^(-1/4))=
=log_(3)(9x^(-1/4)=log_(3)9+log_(3)x^(-1/4)=2-(1/4)log_(3)x
Замена
log_(3)x=t
sqrt(16-3t) больше или равно 2*(2-(1/4)t)
sqrt(16-3t) больше или равно 4-(1/2)t
1)
{4-(1/2)t < 0
{16-3t больше или равно 0
неравенство верно, положительное выражение всегда больше отрицательного.
1)
{t > 8
{t меньше или равно 16/3
cистема не имеет решений
2)
{16-3t больше или равно 0
{16-3t больше или равно (4-(1/2)t)^2 ⇒
{t меньше или равно 16/3
{(1/4)t^2-t меньше или равно 0
{t меньше или равно 16/3
{0 меньше или равно t меньше или равно 4
0 меньше или равно log_(3)x меньше или равно 16/3
1 меньше или равно x меньше или равно 3^5*∛3
О т в е т. [1; 3^5*∛3]