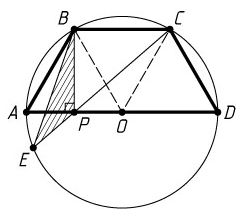
В окружность радиуса 2sqrt{7} вписана трапеция ABCD, причём её основание AD является диаметром, а угол BAD равен 60. Хорда CE пересекает диаметр AD в точке P, причём AP : PD = 1 : 3. Найдите площадь треугольника BPE.
математика 10-11 класс
6226
Пусть O — центр окружности. Тогда треугольники ABO, OBC, COD -- равносторонние, а т.к. P — середина AO, то BP — высота треугольника ABO.
BP = AB·sin 60° = 2·sqrt(7)·sqrt(3) / 2 = sqrt(21),
AP = AB / 2 = sqrt(7).
Поскольку BC = OB = 2·sqrt(7), то
S_(ΔBPC) = BC·BP / 2 = 2·sqrt(7)·sqrt(21) / 2 = 7·sqrt(3).
По теореме Пифагора
PC = sqrt(BC^2+BP^2) = sqrt(28+21) = 7.
По теореме о произведении отрезков пересекающихся хорд AP·PD = EP·PC.
Отсюда находим, что
EP = AP·PD / PC = sqrt(7)·3·sqrt(7) / 7 = 3.
Следовательно,
S_(ΔBPE) = S_(ΔBPC)·PE / PC = 3·7·sqrt(3) / 7 = 3·sqrt(3).
Ответ: 3·sqrt(3)
Вопросы к решению (1)
SΔBPE = SΔBPC·PE / PC почему это так?
Площадь треугольника = 1/2 · основание на высоту
S_(ΔBPC) = 1/2 на основание PC и умноженное на некоторую высоту, проведенную из вершины B к прямой PC
S_(ΔBPE) = 1/2 на основание PE и умноженное на ту же высоту (только тут высота - это перпендикуляр на продолжение основания EP, но это тот же самый отрезок)
