Задача 26841 ...
Условие
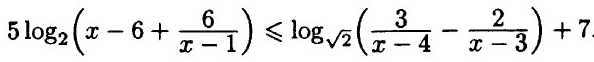
математика 10-11 класс
600
Все решения
ОДЗ:
{(x2–7x+12)/(x–1) > 0
(1;3) U (4;+ ∞)
Так как
log√2y=1/(1/2)log2y=2log2y
y > 0
5log2(x–6+(6/(x–1))=5log2(x2–7x+12)/(x–1)
2log2(3/(x–4)–(2/(x–3))=2log2(x–1)/(x2–7x+12)
5log2(x2–7x+12)/(x–1) ≤ 2log2(x–1)/(x2–7x+12) + 7
5log2(x–3)+5log2(x–4)–5log2(x–1)≤ 2log2(x–1)–2log2(x–3)–2log2(x–3) +7
7log2(x–4)(x–3)/(x–1) ≤ 7
log2(x–4)(x–3)/(x–1) ≤ 1
(x–4)(x–3)/(x–1) ≤ 2
(x2–7x+12–2x+2))/(x–1) ≤ 0
(x2–9x+14)/(x–1) ≤ 0
(x–2)(x–7)/(x–1) ≤ 0
_–__ (1) ____ (2) _____–_____ (7) __________
С учетом ОДЗ получаем ответ.
(4;7)
Обсуждения