Задача 26729 sin^4 x + cos^4 x...
Условие
Перерешиваем: [link=https://reshimvse.com/zadacha.php?id=3882]
Решение
cos^4x=(cos^2x)^2=((1+cos2x)/2)^2
уравнение принимает вид:
((1-cos2x)/2)^2 + ((1+cos2x)/2)^2 + сos2x=0,5
((1-2cos2x+cos^22x)/4) +((1+2cos2x+cos^22x)/4) + сos2x=0,5
((2+2cos^22x)/4)+ сos2x=0,5
1+cos^22x+2cos2x=1
cos2x*(cos2x+2)=0
cos2x=0 ⇒ 2x=(Pi/2)+Pik, k ∈ Z ⇒ x=(Pi/4)+(Pi/2)k, k ∈ Z
или
сos2x=-2 - нет корней, так как |cos2x|меньше или равно 1
О т в е т. (Pi/4)+(Pi/2)k, k ∈ Z 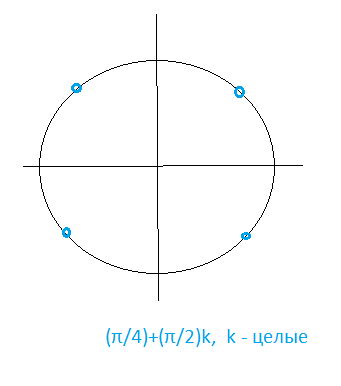
Все решения
sin^4(x)+cos^4(x)+cos2x=0.5
(sin^2(x)+cos^2(x))^2-2sin^2x*cos^2x+cos2x=0.5
1-1/2*sin^2(2x)+cos2x=0.5;
2cos2x-(1-cos^2(2x)=-1;
cos^2(2x)+2cos2x=0;
cos2x*(cos2x+2)=0;
cos2x+2=0-решений нет так как |cos2x| < =1;
cos2x=0.тогда x=pi/4+pi*k/2. k-целое число
Ответ: x=pi/4+pi*k/2. k-целое число
