Задача 26689 4.2.18) Луч света, пройдя через точку...
Условие
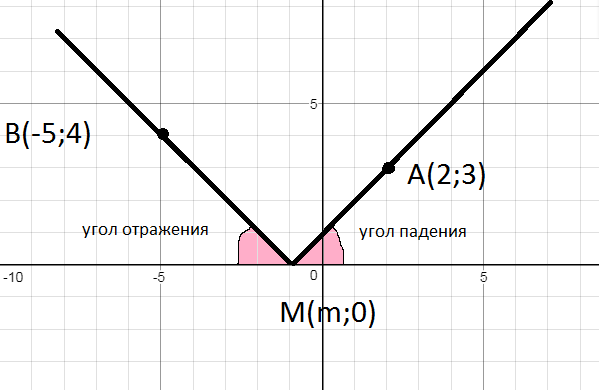
отразился от нее и прошел через точку В(-5; 4). Найти угол а.
Решение
Составим уравнение для прямой проходящей через точку A
y–y_(A)=k(x–x_(A)), где k=tg альфа
y-3=tg альфа(x-2)
y=tg альфаx-2tg альфа+3
Составим уравнение для прямой проходящей через точку B
y–y_(B)=k(x–x_(B)), где k=tg(180°- альфа)=-tg альфа
y-4=tg альфа(x+5)
y=-tg альфаx-5tg альфа+4
Абсциссу точки, в которой эти прямые пересекаются мы не знаем, мы знаем лишь её ординату y=0
Решим систему уравнений
{tg альфаx-2tg альфа+3=0
{-tg альфаx-5tg альфа+4=0
Выражаем из обоих уравнений x
{x=(2tg альфа-3)/tg альфа
{x=(4-5tg альфа)/tg альфа
и приравниваем правые части обоих уравнений друг к другу
(2tg альфа-3)/tg альфа=(4-5tg альфа)/tg альфа
2tg альфа-3=4-5tg альфа
7tg альфа=7
tg альфа=1
альфа=45°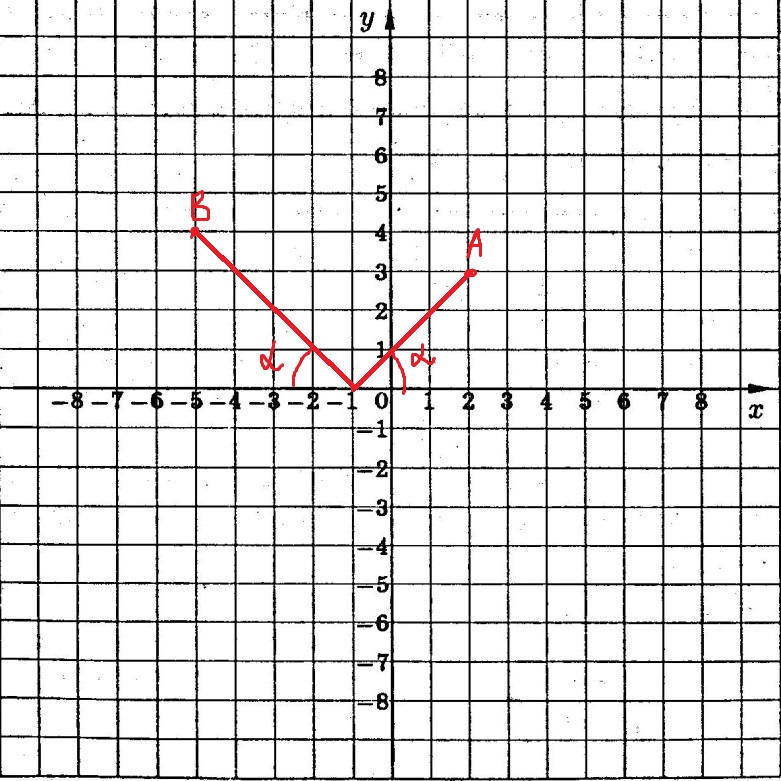
Все решения
Координаты точки М (m;0)
Уравнение прямой АM : у = kx+b_(1)
k- угловой коэффициент прямой,
k=tg альфа,
альфа - угол,который образует прямая АМ с положительным направлением оси Ох.
Так как точки А и M принадлежат прямой АМ, подставим координаты этих точек в уравнение:
3=2k+b_(1)
0=mk+b_(1)
Так как угол падения равен углу отражения, то (180^(o) - альфа) - угол, который образует прямая ВМ с положительным направлением оси Ох.
tg(180^(o)- альфа)=- tg альфа =- k
Уравнение прямой BM: у =- kx+b_(2)
Так как точки В и M принадлежат прямой ВМ, подставим координаты этих точек в уравнение:
4= - k* (-5)+b_(2)
0= -k*m+b_(2)
Cистема:
{3=2k+b_(1)
{0=mk+b_(1)
{4= - k* (-5)+b_(2)
{0= -k*m+b_(2)
Из первого и третьего
{b_(1)=-b_(2)
Складываем второе и четвертое
7 = 7k
k=1
tg альфа = 1
альфа = 45 градусов
О т в е т. 45 градусов