Задача 26647 Все на картинке...
Условие

Все решения
{2x-1 > 0; 2x-1 ≠ 1 ⇒ x ∈ (0,5; 1) U(1;+ бесконечность )
{9x^2-12x+4 > 0 ⇒ (3x-2)^2 > 0 ⇒ x ≠ 2/3
{3x-2 > 0 ⇒ x > 2/3
(6x^2-7x+2 > 0 ⇒ D=49-48=1 x ∈ (- бесконечность;1/2)U(2/3;+ бесконечность )
{3log_(2x-1)(6x^2-7x+2)-2 ≠ 0 ⇒ (6x^2-7x+2)^3 ≠ (2x-1)^2 ⇒
(2x-1)^3*(3x-2)^3 ≠ (2x-1)^2 ⇒ (2x-1)^2*(2x-1)*(3x-2)^3-1) ≠ 0
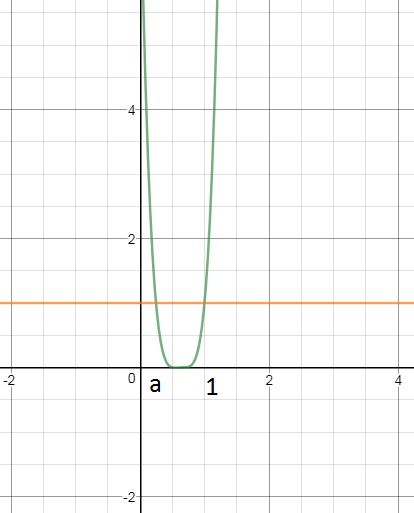
⇒ 2x-1 ≠ 0 или (2x-1)*(3x-2)^3 ≠ 1 ⇒ x ≠ 1 или x ≠ a, 0 < a < 1 и не войдет в ОДЗ
ОДЗ: (3/2; + бесконечность )
В условиях ОДЗ
log_(2x-1)(9x^2-12x+4)=log-(2x-1)(3x-2)^2=2log_(2x-1)(3x-2);
log^2_(2x-1)(9x^2-12x+4)=(2log_(2x-1)(3x-2))^2=4log^2_(2x-1)(3x-2);
log_(2x-1)(6x^2-7x+2)=log_(2x-1)(2x-1)(3x-2)=
=log_(2x-1)(2x-1)+log_(2x-1)(3x-2)=1+log_(2x-1)(3x-2)
Замена переменной
log_(2x-1)(3x-2)=t
Неравенство принимает вид
(4t^2-10t+18)/((3+3t)-2) меньше или равно 2;
(4t^2-16t+16)/(3t+1) меньше или равно 0
так как 4t^2-16t+16 > 0 при любом t ⇒
3t+1 < 0
t < -1/3
log_(2x-1)(3x-2) < -1/3
(2x-1-1)*(3x-2-(2x-1)^(-1/3)) < 0
(2x-2)*(3x-2-(1/∛(2x-1))) < 0
При x ∈ ОДЗ
2x-2 > 0
значит
(3x-2 - (1/∛2x-1)) < 0 ⇒ (3x-2)^3*(2x-1) < 1 см последнее неравенство при нахождении ОДЗ
Решением служит (a;1) , который не входит в ОДЗ
Cм. рис. Графики у=(2х-1)(3х-2)^3 и y=1
О т в е т. Нет решений