Задача 26623 Все на картинке...
Условие
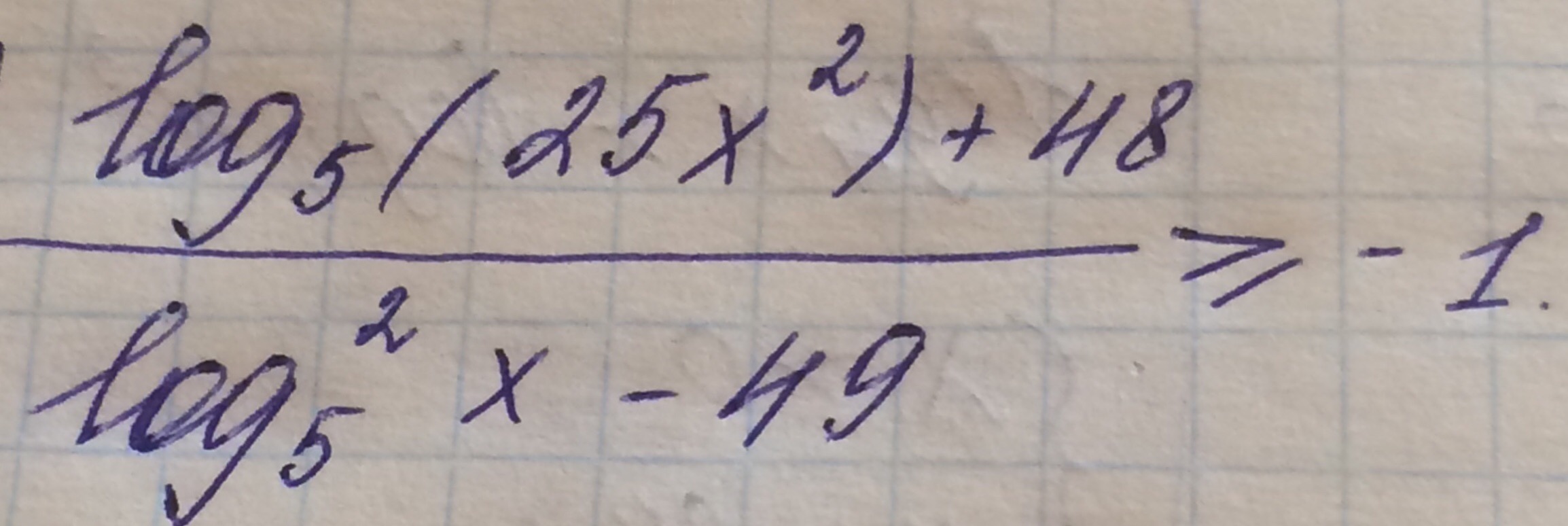
математика 10-11 класс
328
Все решения
log_(5)(25x^2)=log_(5)25+log_(5)x^2=2+2log_(5)|x|В условиях ОДЗ=2+2log_(5)x
Замена
log_(5)x=t
(2+2t+28)/(t^2-49) больше или равно -1 ⇒
(2+2t+28)/(t^2-49) +1 больше или равно 0
(t+1)^2/(t^2-49) больше или равно 0
_+__ ( - 7) ___ [ - 1] ____ (7) _+__
t < - 7 или t= -1 или t > 7
log_(5)x < - 7 ⇒ 0 < x < 1/5^(7)
log_(5)x = - 1 ⇒ x= 1/5
log_(5)x > 7 ⇒ x > 5^7
О т в е т. (- бесконечность; 1/5^7)U {1/5}U (5^7;+ бесконечность )