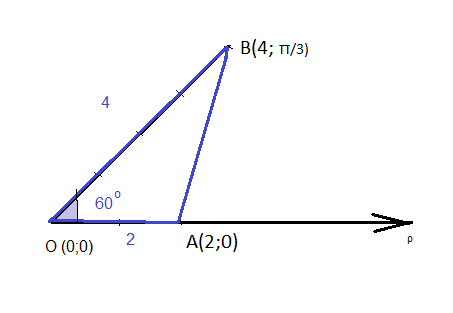
Задача 26615 4.1.54) Одна из вершин треугольника...

slava191

22.04.2018

4.1.54) Одна из вершин треугольника лежит в полюсе полярной си­стемы координат, а другие в точках А(2;0) и В(4; Pi/3); Найти радиус вписанной в треугольник окружности.

SOVA

22.04.2018

★

Δ АОВ:
OA=2
OB=4
∠ AOB=Pi/3=60^(o)

По теореме косинусов
АВ^2=OA^2+OB^2-2*OA*OB*cos ∠ AOB=

=2^2+4^2-2*2*4*(1/2)=12

AB=2sqrt(3)

S( Δ AOB)= (1/2)OA*OB*sin ∠ AOB=(1/2)*2*4*sin 60^(o)=

=2sqrt(3)


p= (OA+OB+AB)/2=(2+4+2sqrt(3))/2=3+sqrt(3)

r=S/p=2sqrt(3)/(3+sqrt(3))=2sqrt(3)*/sqrt(3)*(sqrt(3)+1)=2/(sqrt(3)+1)
или
r=2*(sqrt(3)-1)/((sqrt(3))^2-1)=sqrt(3)-1

О т в е т. r=2/(sqrt(3)+1)=sqrt(3)-1