Задача 26613 4.1.51) Сторона правильного...

slava191

22.04.2018

4.1.51) Сторона правильного шестиугольника равна 1. Приняв за по­люс одну из его вершин, а за полярную ось — сторону, через нее проходящую, найти полярные координаты остальных пяти
вершин.

SOVA

22.04.2018

★

Правильный шестиугольник АВСDEF состоит из шести правильных правильных треугольников
Пусть А(0;0)
Ось проходит через сторону АВ.
Тогда В(1;0)
Из треугольника АВС ∠CABC=30^(o)
∠ABC=120^(o) по теореме косинусов
АС^2=1^2+1^2-2*1*1*cos120^(o)=1+1+1=3
AC=sqrt(3)
С(sqrt(3); Pi/6)

AC=AE

AD=FC=2
FC- ( бо`льшая диагональ правильного шестиугольника)
AD=2
∠DAC=60^(o)
D(2;Pi/3)
E(sqrt(2);Pi/2)

AF=1
=∠FAB=120^(o)
F(1;2Pi/3)

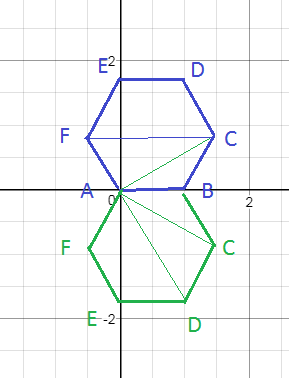
О т в е т. A(0;0); B(1;0) ; C (sqrt(3);Pi/6); D(2;Pi/3); E(sqrt(3);Pi/2); F(1;2Pi/3)
В силу симметрии возможна и вторая серия ответов
A(0;0); B(1;0) ; C (sqrt(3); - Pi/6); D(2;- Pi/3); E(sqrt(3);-Pi/2); F(1; -2Pi/3)