Задача 26594 4.1.37) Даны две смежные вершины...
Условие
Решение
(х–x_(A))/(x_(B)–x_(A))=(y–y_(A))/(y_(B)–y_(A))
(х–2)/(-1–2)=(y–(-1))/(3–(-1))
4*(х-2)=-3(у+1)
4х+3у-5=0 - уравнение АВ
АВ=sqrt((-3)^2+4^2)=5
Уравнения прямых, перпендикулярных АВ
имеют вид 3х-4у+k=0
Одна такая прямая проходит через точку A
Подставим координаты точки А в уравнение 3х-4у+k=0
3*2-4*(-1)+k=0
k=-10
Уравнение АD:
3х-4у-10=0
Расстояние от точки С(x_(C); y_(C)) до прямой AB равно 5
d=|4x_(C)+3y_(C)-5| /5
|4x_(C)+3y_(C)-5| /5=5
Уравнение прямой ВС:
3*(-1)-4*3+k=0
k=15
3x-4y+15=0 - уравнение ВС
Расстояние от точки D(x_(D);y_(D))
до прямой AB равно 5
d=|4x_(D)+3y_(D)-5|/5
|4x_(D)+3y_(D)-5|/5=5
Точка С принадлежит прямой ВС, значит ее координаты удовлетворяют уравнению ВС
3x_(С)-4y_(С)+15=0
Точка D принадлежит прямой AD, значит ее координаты удовлетворяют уравнению AD
3x_(D)-4y_(D)-10=0
Из двух систем:
{|4x_(C)+3y_(C)-5| /5=5
{3x_(С)-4y_(С)+15=0 ⇒ y_(C)=(3x_(C)+15)/4
и
{|4x_(D)+3y_(D)-5|/5=5
{3x_(D)-4y_(D)-10=0 ⇒ y_(D)=(3x_(D)+10)/4
находим координаты точек С и D.
|4x_(C)+(3/4)*(3x_(C)+15)-5|=25
25x_(C)+25 = -100 или 25x_(C)+25=100
25x_(C)=-125 или 25x_(C)=75
x_(C)=- 5 или х_(С)=3
у_(С)=0 или у_(С)=6
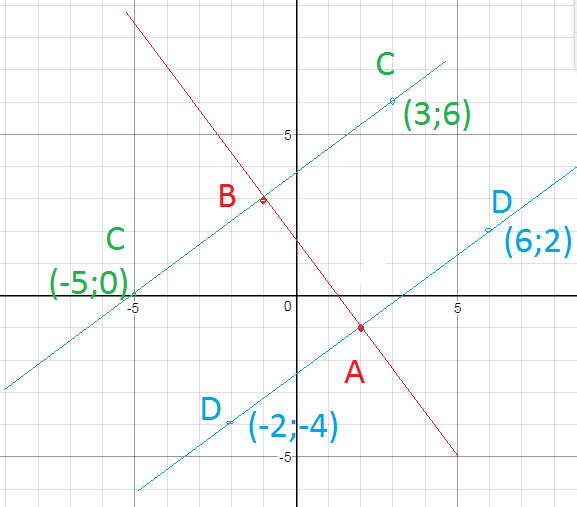
C(3;6) или С (-5;0)
D(6;2) или D(-2;-4)