Задача 25952 Все на картинке...
Условие
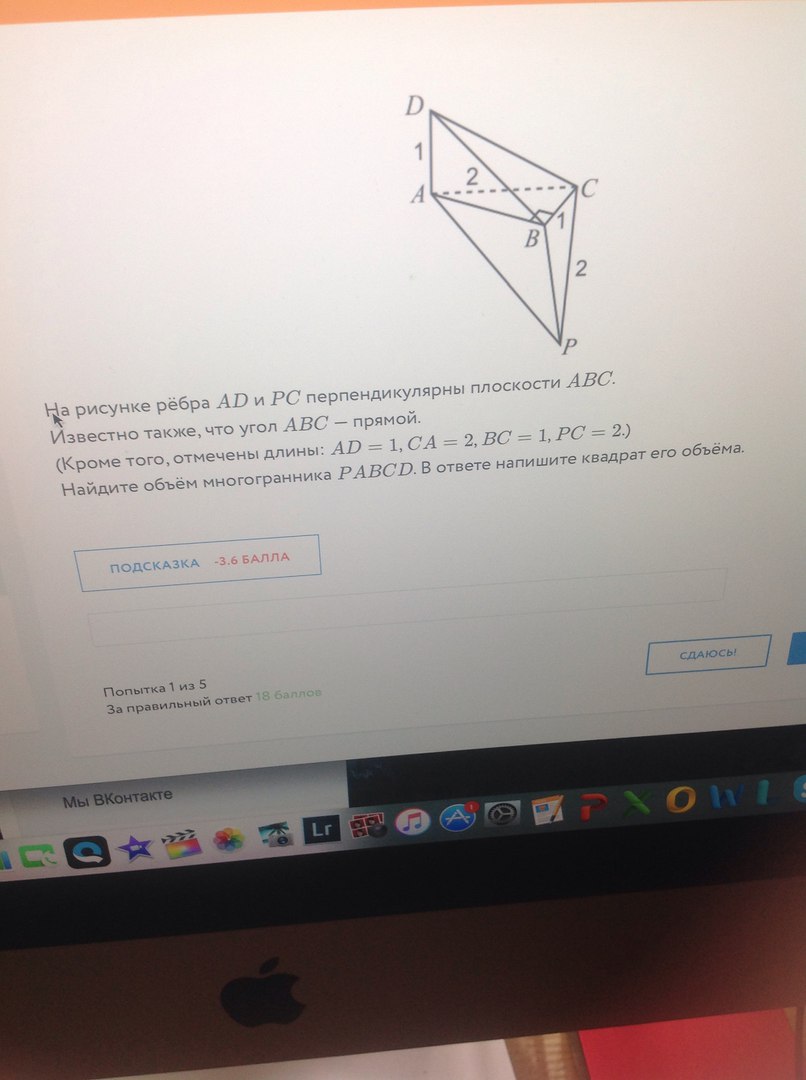
математика 10-11 класс
476
Решение
★
=(1/3)S( Δ ABC)*DA + (1/3)S( Δ ABC)* PC=
=(1/3)*S( Δ ABC)*(DA+PC)
DA=1; PC=2
По теореме Пифагора из треугольника АВС
AB^2=AC^2-BC^2=2^2-1^2=4-1=3
AB=sqrt(3)
S( Δ ABC)=(1/2)AB*BC=(1/2)*sqrt(3)*1=sqrt(3)/2
V(PABCD)=sqrt(3)/2