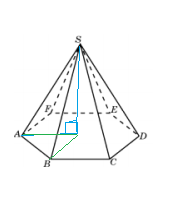
Задача 25682 Объем правильной шестиугольной пирамиды...

slava191

31.03.2018

Объем правильной шестиугольной пирамиды 6. Сторона основания равна 1. Найдите боковое ребро.

SOVA

31.03.2018

★

V( пирамиды) = (1/3)*S(осн.)*Н
S(шестиугольника)=6*S( Δ AOB)=6*(a^2*sqrt(3)/4)
где а - сторона правильного шестиугольника.
при а=1
S=3sqrt(3)/2

H=3V/S(осн.)=4sqrt(3)

По теореме Пифагора
SA^2=SO^2+OA^2=(4sqrt(3))^2+1^2=48+1=49
SA=7

О т в е т. 7