Задача 2498 В системе, показанной на рисунке, m1=m,...
Условие
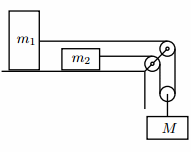
физика 10-11 класс
4180
Решение

Ответ: 5
Все решения


Ответ: 5