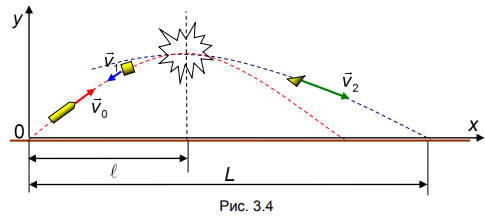
Снаряд, вылетевший из орудия под некоторым углом к горизонту, разорвался в высшей точке траектории на два одинаковых осколка. Первый осколок вернулся в точку, из которой был выпущен снаряд. На каком расстоянии от места выстрела упал второй осколок, если расстояние по горизонтали от места выстрела до места взрыва равно (см. рис. 3.4)?
физика ВУЗ
15750
В силу кратковременности взрыва снаряда действием силы тяжести в процессе взрыва можно пренебречь и считать систему «снаряд и осколки» изолированной. В верхней точке траектории скорость снаряда направлена горизонтально. Следовательно, то же направление имеет и импульс системы. Поскольку первый осколок возвращается в точку выстрела, то его скорость непосредственно после взрыва равна по величине и противоположна по направлению скорости снаряда перед взрывом. С учетом сделанных замечаний закон сохранения импульса в проекции на горизонтальное направление имеет вид

Ответ: В решение



