Задача 24667 а) Решите уравнение...

slava191

07.03.2018

а) Решите уравнение

sin2x-2sqrt(3)cos(x+(7Pi)/6)=3cosx.

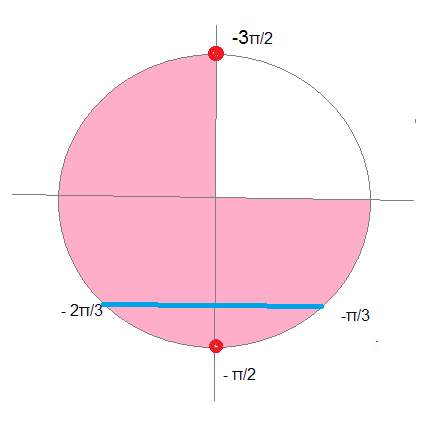
б) Укажите корни этого уравнения, принадлежащие отрезку [-(3Pi)/2;0]

SOVA

07.03.2018

★

sin2x=2sinx*cosx;
cos(x+(7π)/6)=cosx*cos(7Pi/6) - sinx*sin(7Pi/6)=
=-(sqrt(3)/2)cosx+(1/2)*sinx

Уравнение принимает вид
2sinx*cosx+3cosx-sqrt(3)sinx-3cosx=0
2sinx*cosx-sqrt(3)sinx=0
sinx*(2cosx-sqrt(3))=0
sinx=0 ⇒ x=Pin, n ∈ Z
ИЛИ
cosx=sqrt(3)/2
x=±(Pi/6)+2Pik, k ∈ Z

О т в е т. Pin; ±(Pi/6)+2Pik, n, k ∈ Z

б) Отрезку [-(3Pi/2);0] принадлежат корни
-Pi; -Pi/6; 0