Задача 24474 Л16) Через вершины А и В треугольника...

slava191

03.03.2018

Л16) Через вершины А и В треугольника АВС проведена окружность радиуса 2sqrt(5), отсекающая от прямой ВС отрезок 4sqrt(5) и касающаяся прямой АС в точке А. Из точки В проведен перпендикуляр к прямой ВС до пересечения с прямой АС в точке F.

А) Докажите AF=BF

Б) Найдите площадь треугольника АВС, если BF=2.

SOVA

04.03.2018

★

1) рис.1 ВС=2R - диаметр окружности.
BF ⊥ BC
AF ⊥ OA
По свойству касательных, проведенных из точки F отрезки касательных равны.
AF=BF
Из прямоугольного треугольника OAF:
tg ∠ OFA=OA/FA=2sqrt(5)/2=sqrt(5)
Δ OBF = ΔOAF по двум катетам
FO - биссектриса
Применяем формулу тангенса двойного угла
tg ∠ BFA=2tg∠ OFA/(1-tg^2∠ OFA)=2sqrt(5)/(1-5)=-sqrt(5)/2 < 0
Значит, ∠ BFA > Pi/2
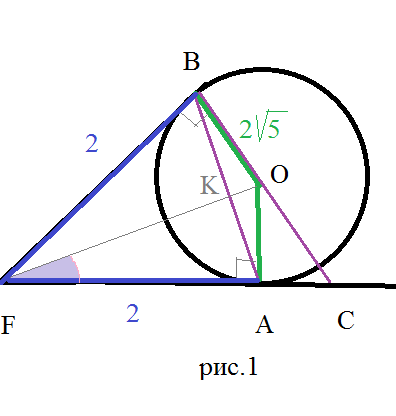
∠ BFA - тупой, что не соответствует рис.1

2)
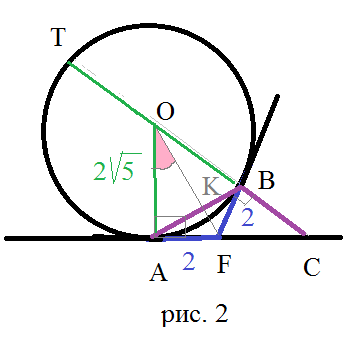
см. рис. 2
продолжение стороны ВС
ВТ=2R

ОА=ОВ=2sqrt(5)
AF=BF=2
Из прямоугольного треугольника AOF
tg ∠ AOF=AF/AO=2/2sqrt(5)=1/sqrt(5)
Прямоугольные треугольники AOF и BOF равны по двум катетам.
OF- биссектриса
По формуле тангенса двойного угла:
tg ∠ AOC=2*tg ∠ AOF/(1-tg ^2∠ AOF)=sqrt(5)/2
cos^2∠ AOC=1/(1+tg^2 ∠ AOB)=1/(1+5/4)=4/9
cos∠ AOC=2/3
cos∠ AOC=OA/OC ⇒ OC=OA/cos ∠ AOC=3sqrt(5)

BC=OC-OB=3sqrt(5)-2sqrt(5)=sqrt(5)

По теореме Пифагора из прямоугольного треугольника BFC:
FC^2=BC^2+BF^2=(sqrt(5))^2+2^2=9
FC=3
AC=5
S( Δ ABC)=(1/2)AC*BC*sin ∠ ACO=
=( sin ∠ ACO=cos ∠ AOC=2/3)=
=(1/2)*5*sqrt(5)*(2/3)=5sqrt(5)/3

О т в е т. 5 sqrt(5)/3