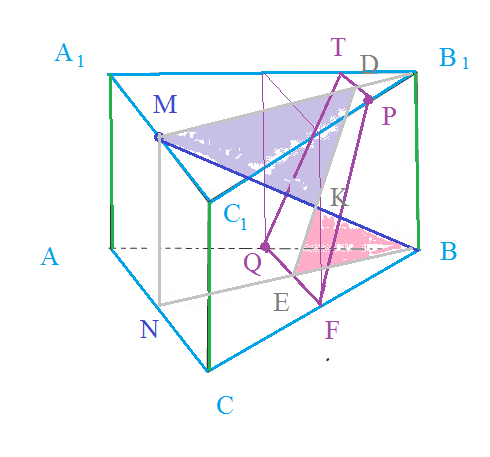
Задача 24473 Л14) Сторона основания правильной...

slava191

03.03.2018

Л14) Сторона основания правильной треугольной призмы АВСА1В1С1 равна 10sqrt(3), а высота СС1 равна 7,5. На ребре В1С1 отмечена точка Р так, что В1Р:РС1=1:3. Точки Q и М являются серединами сторон АВ и А1С1 соответственно. Плоскость альфа параллельна прямой АС и проходит через точки Р и Q.

А) Докажите, что прямая ВМ перпендикулярна плоскости альфа
Б) Найдите расстояние от точки М до плоскости альфа

SOVA

04.03.2018

★

a)
Сечение PTQF - равнобедренная трапеция
PT || A1C1
PT=(1/4) A1C1
QF || AC
QF=(1/2)AC
QF- средняя линия треугольника АВС
QF=5sqrt(3)
TP=(1/2)QF=5sqrt(3)/2

NB=MB1=asqrt(3)/2=10sqrt(3)*(sqrt(3)/2)=15 - высоты равностороннего треугольника

МB^2=MN^+NB^2=7,5^2+15^2=15sqrt(5)/2


DE - высота равнобедренной трапеции, боковые стороны которой QT=PF=sqrt(7,5^2+(5sqrt(3)/2)^2)=sqrt(75)=5sqrt(3)

DE=15sqrt(5)/4 из прямоугольной трапеции DB1BE

Из подобия треугольников MKD и KEB
DK/KE=MD/BE=(3/4h)/(h/2)=(3/2) ⇒

DE=DK+KE=(3/2)KE+KE=(5/2)KE
15sqrt(5)/4=(5/2) KE
KE=3sqrt(5)/2
DK(3/2)*KE=(3/2)*3sqrt(5)/2=9sqrt(5)/4

MK/KB=MD/BE=(3/4h)/(h/2)=(3/2) ⇒
KB=(2/3)MK
MK+KB=MB
MK+(2/3)MK=15sqrt(5)/2
MK=9sqrt(5)/2

MD^2=MK^2+KD^2
(45/4)^2 =(9sqrt(5)/2)^2+(9sqrt(5)/4)^2 - верно, значит по теореме обратной теореме Пифагора, треугольник MKD - прямоугольный, угол MKD - прямой
MK ⊥ KD

BN⊥ QF
MN ⊥ пл. АВС, значит MN ⊥ OF
QF перпендикулярна двум пересекающимся прямым плоскости MNB1B, значит QF⊥ пл MNB1B
Плоскость α проходит через перпендикуляр QF к плоскости MNB1B, плоскость α и пл. MNB1B взаимно перпендикулярны.
Значит QF ⊥ MB

MK ( а значит и MB)⊥DE ,MB ⊥ QF

MB⊥ пл. α

б)
MK=9sqrt(5)/2

О т в е т. MD = 9sqrt(5)/2