Задача 24471 Л13) а) Решите уравнение:...

slava191

03.03.2018

Л13) а) Решите уравнение: cos2x+3sqrt(2)sinx-3=0

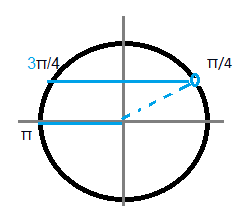
б) Укажите корни этого уравнения, принадлежащие отрезку (Pi/4; Pi]

SOVA

03.03.2018

★

сos2x=1-2sin^2x

1-2sin^2x+3sqrt(2)sinx-3=0;
2sin^2x-3sqrt(2)sinx+2=0
D=(-3sqrt(2))^2-4*2*2=18-16=2

sinx=(3sqrt(2)-sqrt(2))/4=sqrt(2)/2
x=(-1)^k(Pi/4)+Pik, k ∈ Z
ИЛИ
sinx=(3sqrt(2)+sqrt(2))/4=sqrt(2)
уравнение не имеет корней, |sinx| меньше или равно 1

О т в е т.
а) (-1)^k(Pi/4)+Pik, k ∈ Z
б) указанному промежутку принадлежит
х=3Pi/4