Задача 24443 Полностью исследовать функции(чертить...
Условие
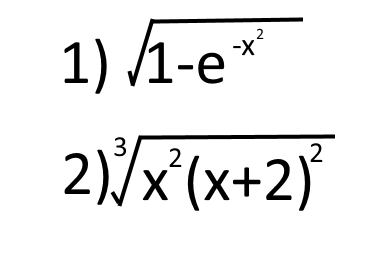
Решение
1)Область определения
1 - e^(-x^2) больше или равно 0 ⇒ e^(-x^2) меньше или равно 1 ⇒ -x^2 меньше или равно 0 ⇒
x ∈ (- бесконечность;+ бесконечность)
2)y`=(1-e^(-x^2))`/2sqrt(1-e^(-x^2))= x*e^(-x^2)/sqrt(1-e^(-x^2))
y`=0
x=0
__- ____ (0) __ +___
Функция убывает на (- бесконечность ;0)
и возрастает на (0;+ бесконечность =
х=0 - точка минимума
y(0)=sqrt(1-e^(0))=sqrt(1-1)=sqrt(0)=0
2.
1) область определения (- бесконечность; + бесконечность )
2)y`=(x^(2/3)*(x+2)^(2/3))`=
=(x^(2/3))`*(x+2)^(2/3) + (x^(2/3))*((x+2)^(2/3))` =
=(2/3)*x^(-1/3)*(x+2)^(2/3) + (x^(2/3))*(2/3)((x+2)^(-1/3))=
= (2/3)x^(-1/3)*(x+2)^(-1/3)*(x+2+x)
y`=0
2x+2=0
x=-1
__-__ (-2) _ + _ (-1) _ -_ (0) _ +__
Функция убывает на (- бесконечность ; -2) и на (-1;0)
и возрастает на (-2;-1) и на (0;+ бесконечность )
х= - 1 - точка максимума
y(- 1)=∛((-1)^2*(-1+2)^2)=1
х=-2 и х=0 - точки минимума
y(-2)=y(0)=0
