Задача 24442 Помогите решить геометрическую задачу по...

vk142633359

02.03.2018

Помогите решить геометрическую задачу по матану на min max. ''Найти уrлы треугольника AвС с большим периметром, даны основание треугольника BC = (альфа) и противолежащий ему угол < BAC = ( бетта)''

SOVA

02.03.2018

★

Пусть один угол х, третий - (Pi - бета -х)
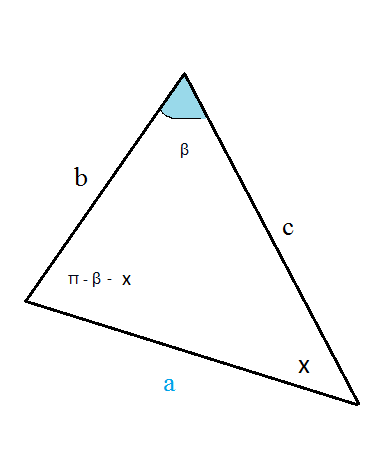
По теореме синусов стороны пропорциональны синусам противолежащих улов:
a/sin бета = b/sinx
Поэтому вторая сторона b=asin x/sin бета
a/sin бета = c/sin(Pi-бета -x)
sin(Pi - бета -х)= sin( бета +x)
третья сторона с=asin (бета + x)/sin бета

P(x)=a+b+c=a+a*(sinx/sin бета) +a*(sin( бета +x)/sin бета)=

=(a/sin бета )*(1+sinx+sin( бета +x))

P`(x)=(a/sin бета )*(cosx+cos( бета +x))

P`(x)=0
cosx+cos( бета +x)=0
2cos(x+ (бета/2))*cos(- бета /2)=0
cos(x+ (бета/2))=0
x+ (бета/2)=Pi/2
x=(Pi/2)-(бета /2)

Третий угол
Pi- бета -((Pi/2)-( бета /2))=

=(Pi/2)- бета +(бета/2)