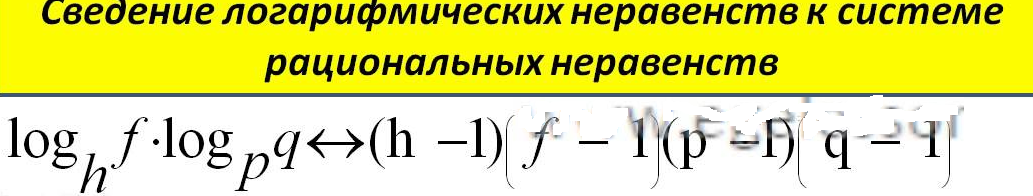Задача 24407 Все на картинке...
Условие
математика
433
Все решения
{2-5x > 0; 2-5x ≠ 1 ⇒ (- бесконечность ;1/5)U(1/5;2/5)
{5x+2 > 0 ⇒ x > - 2/5
{5x+3 > 0 ; 5x+3 ≠ 1 ⇒ x > - 3/5; x ≠ -2/5
{3-5x > 0 ⇒ x < 3/5
ОДЗ: х ∈ (-2/5;1/5) U (1/5;2/5)
На ОДЗ с помощью метод рационализации логарифмических неравенств ( см. приложение) данное неравенство равносильно неравенству
(2 - 5х - 1)*(5х + 2 - 1)*(3 - 5х - 1)* (5х + 3 - 1) меньше или равно 0
(1 - 5х)(5х + 1)*(2 - 5х)*(5х + 2) меньше или равно 0
(5х - 1) * (5х + 1) * (5х + 2)* ( 5х - 2) меньше или равно 0
(-2/5) __-__ [-1/5] ___+___ (1/5) _-_ (2/5)
О т в е т. [-1/5;1/5)