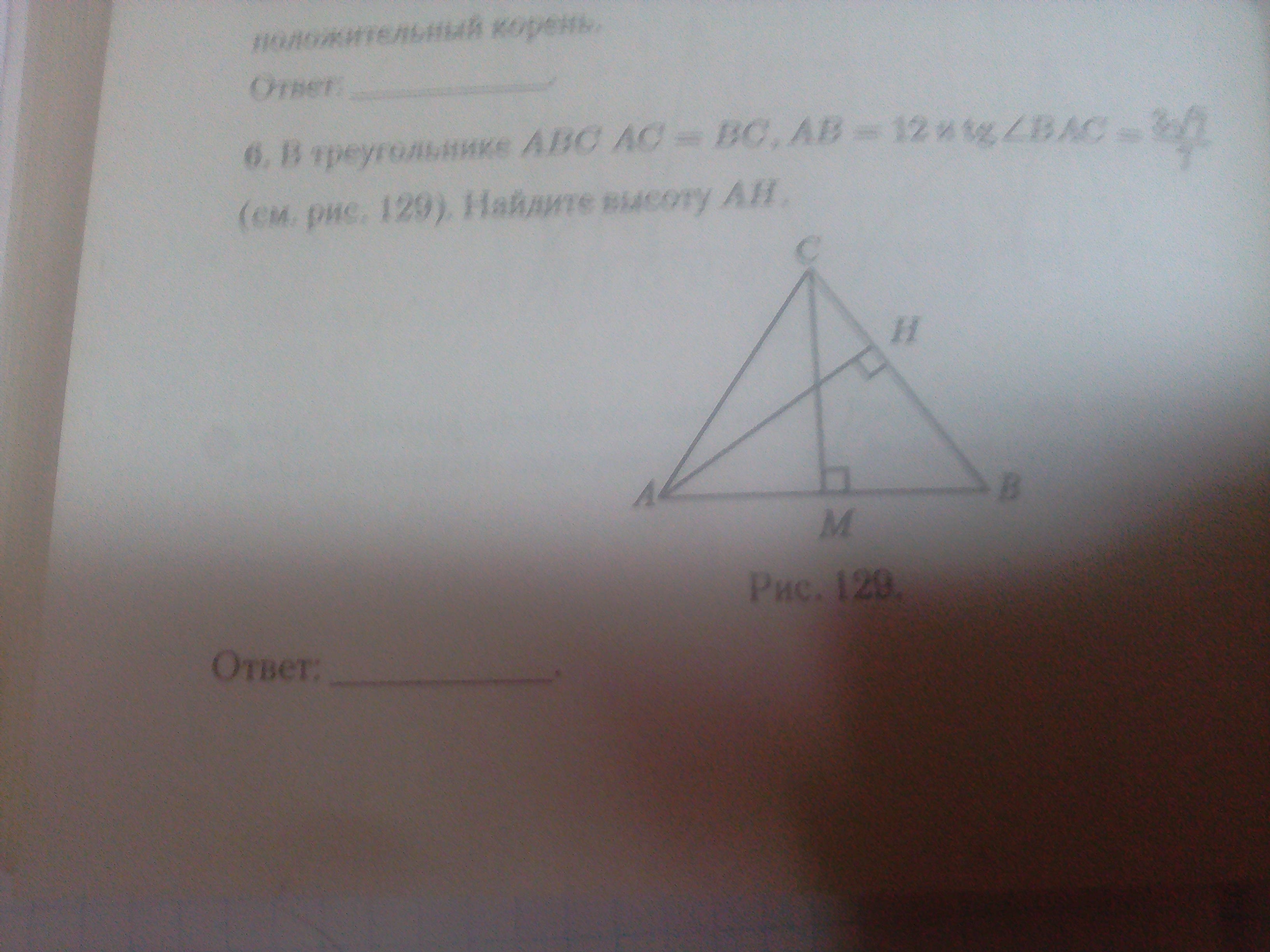
Задача 24310 6. В треугольнике ABC AC = BC, AB = 12 и...

u8526235135

27.02.2018

6. В треугольнике ABC AC = BC, AB = 12 и BAC = 3sqrt(7)/7, (см. рис. 129). Найдите высоту AH.

SOVA

27.02.2018

★

АМ=МВ=6
Из треугольника АCМ
tg ∠ CAM=CM/AM
CM=AM*tg∠ CAM=6*3sqrt(7)/7=18sqrt(7)/7
AC^2=AM^2+CM^2=6^2+(18sqrt(7)/7)^2=36+(324/7)
AC=sqrt(576/7)=24/sqrt(7)

S (Δ ABC) = (1/2)AB*CM и S (Δ ABC) = (1/2)BС*АН

AB*CM = BС*АН

АН=(12*18sqrt(7)/7)*(sqrt(7)/24)=9