Задача 24120 ...
Условие
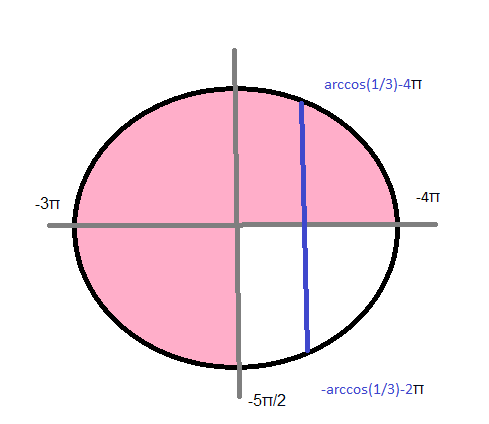
б) [-4π, -5π/2]
математика 10-11 класс
808
Решение
★
cosx ≠ 0
cosx ≠ 1/2
(4cosx-5)*cosx + 1=2*(2cos^2x-cosx)
cosx=1/3
x= ± arccos(1/3)+2Pik, k ∈ Z
корни удовлетворяют ОДЗ
Указанному промежутку принадлежит корень
x=arccos(1/3)-4Pi