Задача 23917 ((4^x-3)log4(17-2^x))/log16(x)-log4(2)*tg(x/2)=...
Условие
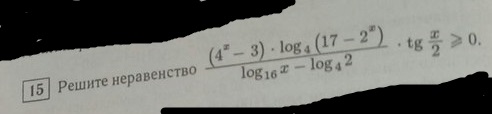
Решение
{x > 0
{17-2^x > 0 ⇒ 2^x < 17 ⇒ x < log_(2)17
x≠( Pi/2)+Pim,m∈ Z⇒ x ≠ ( Pi)+2Pim, m∈ Z
[red]ОДЗ: [/red]x ∈ (- ∞ ; log_(2)17) и на этом интервале "дырки" в точках вида
х=π+2πm, m∈ Z
log_(2)17 < log_(2)16=4 < 2π
Поэтому самая правая "дырка" в точке π
Применяем обобщенный метод интервалов.
Находим нули числителя:
4^x-3=0
x=log_(4)3
0 < log_(4)3 < log_(4)4 =1
log_(4)(17-2^x)=0
17-2^x=1
2^x=16
x=4
tg(x/2)=0
(x/2)=Pik, k ∈ Z
x=2Pik, k ∈ Z
Находим нули знаменателя
log_(16)x-log_(4)2=0
(log_(4)x/log_(4)16)-log_(4)2=0
log_(4)(sqrt(x)/2)=0
x=4
Расставляем знаки:
(0) _+__ [log_(4)3] _-_ (Pi) __+__ (4) _+_ (log_(2)17)
О т в е т. (0;log_(4)3]U(Pi;4)U(4;log_(2) 17)